Generar números aleatorios no es fácil para los ordenadores, inherentemente deterministas. Por eso se trabaja en algoritmos que permitan generarlos cumpliendo con diferentes definiciones de aleatoriedad y a la vez ciertas premisas: que no requieran mucha memoria, que el código sea rápido y no demasiado complejo y que los resultados sean «reproducibles» (por ejemplo en simulaciones). Esto último es en cierto modo un poco paradójico, pero es así como funcionan: una vez iniciado un generador con un valor dado debería generar siempre la misma secuencia.
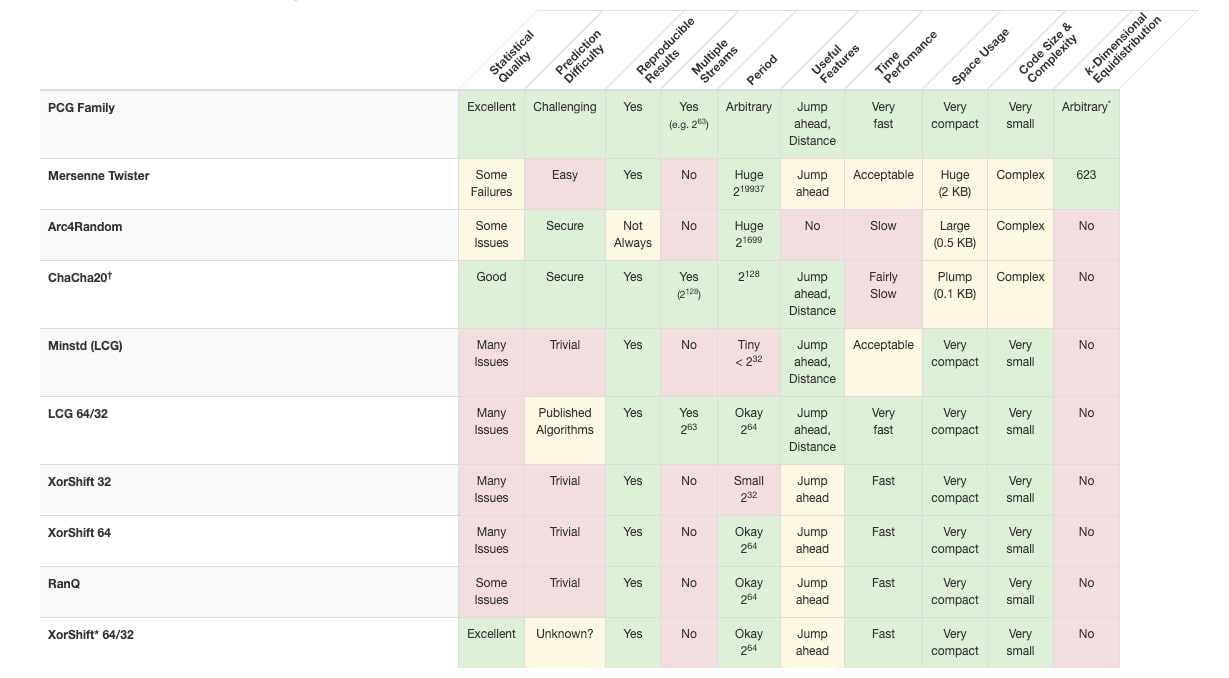
En la página dedicada a la familia PCG de generadores de números aleatorios hay una interesante tabla que muestra todas estas características para los diversos algoritmos que se utilizan habitualmente: Mersenne, ARC4Random, LCG 64/32, XorShift 32/64, RanQ… El propio PCG, explicado en este paper dice ser una solución que cubre con todas las necesidades:
El nombre de la familia, PCG, significa generador congruente permutable. Combina los dos conceptos que subyacen en el esquema de generación, a saber: las funciones de permutación en tuplas y se emplea un generador congruente lineal.
Toda la documentación y el blog que está en esa misma página son interesantes para entender algunos de los problemas actuales: que los generadores de números aleatorios no son suficientemente aleatorios, que algunos son demasiado predecibles o inseguros, lentos o que no tienen funciones que serían muy útiles como el «saltar hacia adelante» (jump ahead). El código está disponible en C y C++.
Las aplicaciones de los generadores de números aleatorios van mucho más allá de usarlos en juegos y simulaciones: también juegan un papel importante en criptografía y seguridad. Si se utilizan generadores inseguros puede que un buen algoritmo criptográfico no sirva de nada o sea fácilmente vulnerable; de ahí su importancia.
Relacionado:
- Las matemáticas de la generación de números pseudoaleatorios
- Una nuevo generador cuántico de números aleatorios
- Un generador de números aleatorios alimentado por muones
- Código para comprobar la aleatoriedad de secuencias aleatorias
- Generadores de números aleatorios que no se ven tan aleatorios
- Un generador de movimientos, ruidos y números aleatorios
- Cuán pésima es nuestra capacidad mental para generar aleatoriedad
- Números aleatorios (y Pi)
- Un millón de dígitos aleatorios, el libro
- HotBits: números verdaderamente aleatorios desde el mundo cuántico
- Los seres humanos no somos muy buenos generando secuencias aleatorias
- La elusiva aleatoriedad, o cómo hacer que el azar intervenga en los algoritmos
- Lámparas de lava, péndulos y partículas para lograr la aleatoriedad
- Puertas traseras de la NSA en algoritmos matemáticos