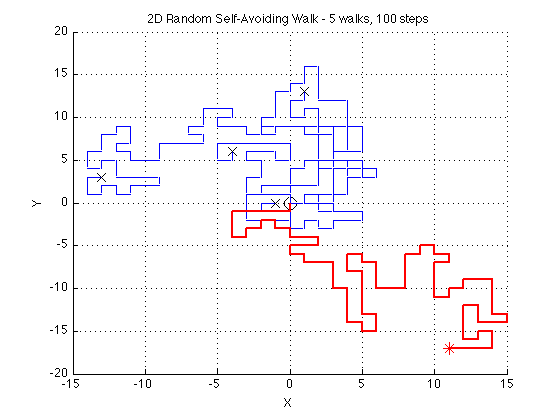
Dos personas están en un gran estadio lleno de gente, se separan y se pierden. Quieren encontrarse la una a la otra, pero no han acordado nada de antemano; la única forma que tienen de localizarse es deambular buscándose. Tal vez una de las persona piense que es mejor quedarse quieta y esperar a que aparezca la otra, pero lo mismo podría suceder a la inversa – por lo que quedarían ambas absurdamente paradas y no se encontrarían nunca. Pero si no dejan de caminar de un lugar a otro tampoco pueden «descartar» lugares por los que ya hayan, pues quizá la otra persona reaparezca tiempo después. ¿Cuál es pues la mejor estrategia para encontrarse?
Hay muchas aproximaciones a este entretenimiento matemático; una de ellas consiste en plantear estrategias y ejecutar simulaciones a ver qué sucede. Idealmente se puede utilizar una matriz cuadrada y suponer, por ejemplo, que las dos personas se «encuentran» si ocupan casillas adyacentes. Y se pueden usar diferentes tamaños para el escenario, «programar» los personajes con algoritmos para recorrer patrones en forma de cuadrados, espiral… Ya lo hizo Rhett Allain para Wired. Hay un sinfín de posibilidades.
Lo importante es que el mismo razonamiento debe usarse para ambas personas, pues se entiende que no tienen forma de comunicarse (cuando se inventó este problema no había Whatsapp ;-) ni han acordado nada de antemano.
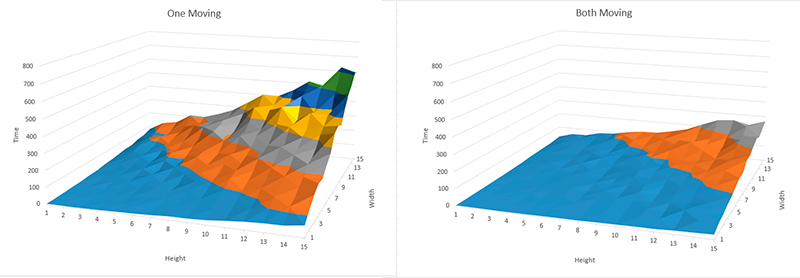
Una de las simulaciones más sencillas muestra cómo varía el tiempo para encontrarse dependiendo de si hay una sola persona moviéndose o si ambas se mueven. Según se ve parece una gran ventaja en que ambos se muevan a la vez pues cuando solo se mueve una a veces el tiempo pasa y pasa sin que se encuentren.
Hace tiempo en un artículo de Nautilus fueron un poco más allá: la recomendación era, literalmente, «empezar emborrachándose para generar unos recorridos realmente aleatorios tras comenzar la búsqueda» (véase: The Man Who Invented Modern Probability: Andrei Kolmogorov). Según el célebre matemático ese «paseo del borracho» o camino aleatorio es la mejor opción para el problema planteado, pues maximiza el área de exploración sin una gran probabilidad de volver al punto inicial.
(Según me parecía recordar otra opción aún mejor era conocer toda esta información de antemano y dedicar la mitad del tiempo a caminar buscando y la otra mitad a permanecer parado. Sin embargo no he encontrado referencias a esto, así que tal vez no sea correcto.)
Otro dato curioso es que este tipo de búsquedas aleatorias depende a veces de otros factores. Por ejemplo, un borracho buscando un bar en la «matriz bidimensional» de las calles de una ciudad es probable que lo encuentre. Pero en el caso equivalente en tres dimensiones, por ejemplo un pájaro buscando su nido, es más probable que no lo encuentre nunca, simplemente por el cambio que supone el paso de 2D a 3D.



