Bassel El Mabsout tiene este curiosísimo artículo sobre los politopos regulares que son básicamente figuras geométricas con un alto grado de simetría. Estos objetos matemáticos pueden existir en diversas dimensiones. Una de sus características es que tengan caras planas; por eso el círculo o una esfera no se consideran politopos.
El dato simpático es la extraña secuencia del número de politopos que hay en cada dimensión, empezando por 0D y pasando por 2D, 3D, 4D… Es esta:
1 1 ∞ 5 6 3 3 3…
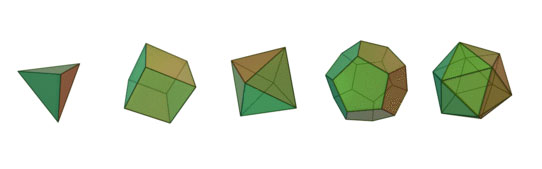
Efectivamente en cero dimensiones (0D) el único politopos posible es un punto, así que sólo hay uno. En 1D es un segmento lineal, de modo que también es único. En el plano 2D en cambio hay infinitos politopos: el triángulo, el cuadrado, pentágono, etcétera. En 3D sabemos desde la antigüedad que sólo hay 5 sólidos platónicos en forma de poliedros convexos con caras y ángulos iguales.
Un poco más allá, en 4D, hay 6 politopos regulares: el pentácoron, el teseracto, el hexadecacoron, el icositetracoron, el hecatonicosacoron y el hexacosicoron. Cinco de ellos son similares a extensiones de los poliedros regulares en 3D (tetraedros o cubos «pegados» unos con otros), pero el icositetracoron (también llamado «24 celdas») es un poco más raro y no tiene equivalente.
La otra curiosidad es que a partir de 5D el número de politopos regulares pasa a ser únicamente 3. Esto que hace que la secuencia del número de politopos que hay en cada dimensión sea realmente extraña, con una subida hasta el infinito y luego una bajada hasta el 3.
§
Y hablando de secuencias no puedo dejar de mencionar esta otra que vi mencionar a @Pickover:
0!!! = 1
1!!! = 1
2!!! = 2
3!!! = 2,6 × 101746 =

Mientras que los tres primeros valores están «contenidos», el cuarto valor de la secuencia, el factorial del factorial del factorial de 3 = ((3!)!)!, se desboca pegando un salto de tamaño descomunal.