17 ecuaciones que cambiaron el mundo, o por qué sí sirve de mucho estudiar matemáticas y ciencia

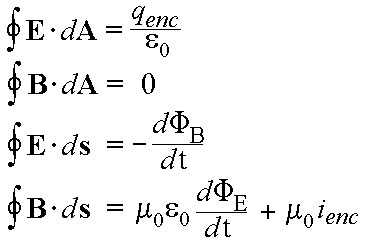
Las ecuaciones de Maxwell, por poner un ejemplo, nos permiten explicar cómo se trasmite la información para la televisión, Internet y los teléfonos, cuánto tarda en llegar la luz de las estrellas, cuál es la base del funcionamiento de las neuronas o cómo opera cualquier central eléctrica, además de otros miles de fenómenos que experimentamos en nuestra vida cotidiana.

Las prisas no son buenas consejeras, así que quiero creer que un desafortunado artículo publicado hace unos días que defiende que estudiar matemáticas sólo sirve para estudiar matemáticas es en realidad fruto de las prisas por entregarlo.

Pero por si acaso me parece adecuado recuperar esta lista de 17 ecuaciones que cambiaron el mundo, con sus correspondientes enlaces, publicada ya hace algún tiempo en Principia Marsupia en la anotación Cómo 4 ecuaciones cambiaron el mundo:

1. El teorema de Pitágoras, porque conectó el álgebra y la geometría.
2. La suma de logaritmos, porque permitió simplificar operaciones muy complejas.
3. El teorema fundamental del cálculo, porque toda las matemáticas de la física reposan sobre él.
4. La teoría de la gravitación de Newton, porque unificó en una sola ecuación fenómenos en apariencia tan diferentes como la caída de una manzana y las órbitas de los planetas.
5. El cuadrado de la unidad imaginaria, porque el análisis complejo es esencial para resolver muchos problemas.
6. La fórmula de Euler para los poliedros, porque representa el nacimiento de la topología.
7. La distribución Gaussiana, uno de los pilares de la estadística.
8. La ecuación de onda, porque unifica fenómenos tan dispares como la luz, el sonido o los terremotos.
9. La transformada de Fourier, esencial en el tratamiento de señales.
10. La ecuación de Navier-Stokes, la base de la aerodinámica y la hidrodinámica.
11. Las ecuaciones de Maxwell, que describen el electromagnetismo.
12. La segunda ley de la termodinámica y el incremento de la entropía.
13. La identidad masa-energía de Einstein, que unifica masa y energía.
14. La ecuación de Schrödinger, que describe la evolución de un sistema cuántico.
15. La entropia de la información de Shannon, que describe el límite hasta el que se puede comprimir la información.
16. El modelo logístico, quizás el sistema más simple donde aparece el caos.
17. El modelo de Black-Scholes, que se utiliza en banca para calcular el precio de productos financieros derivados.

Como extra bonus, 25 respuestas a la pregunta ¿para qué sirven las matemáticas?

(Vía @lolamenting).