No se puede cuadrar un círculo, esto es, dibujar un cuadrado, utilizando únicamente regla y compás, que tenga la misma superficie que un círculo determinado. Es uno de los más clásicos problemas irresolubles de la geometría y las matemáticas.
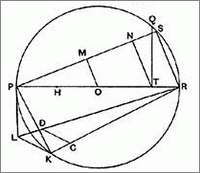
Pero sí que se puede obtener una buena aproximación, como la de esta explicación de Stuart Sasvory: How to square the circle. En esta construcción el segmento RD mide ~1,7724539 que es una aproximación a la raíz cuadrada de π mediante la tradicional fracción 355/113.
Esta aproximación es tan buena que es precisa hasta el séptimo decimal, de modo que un cuadrado de lado RD es casi, casi, un cuadrado perfecto respecto a un círculo de radio OR como el de la imagen.
Tiene tanta precisión que si se dibujara un círculo de cinco kilómetros de diámetro con un lápiz extrafino de tan solo 0,2 milímetros se podría dibujar el cuadrado de superficie equivalente sin que se apreciera ese pequeño error.
Mirando cosas sobre esto encontré este bonito artículo de Isaac Asimov: De los números y su historia: Herramientas del oficio, donde se cuenta algo más sobre la historia de la cuadratura del círculo.
