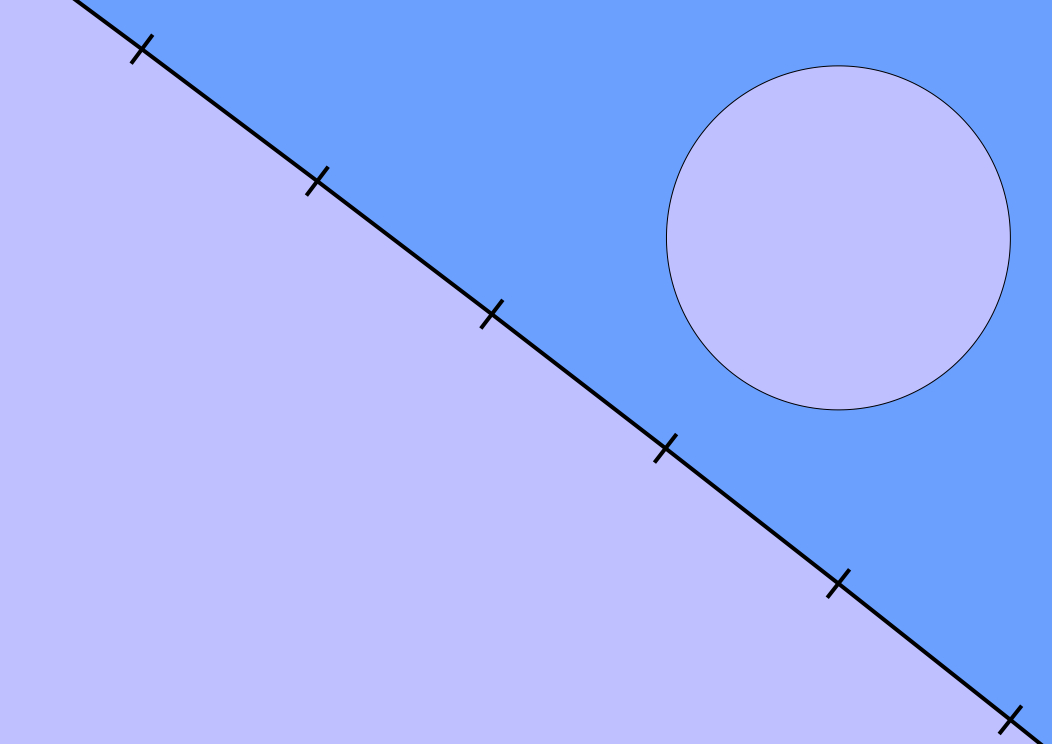
Es difícil dibujar un chiliágono regular con precisión en una pantalla pixelada: parece un círculo
(abajo, contorno ampliado). Imagen: Cmprince (CC) Wikimedia Commons
Me encontré así de repente con una referencia a un polígono regular interesante, que bien podría pasar a engrosar las listas de «favoritos» de muchos aficionados a las matemáticas y la geometría: el chiliágono regular (también llamado kiliágono). Es un polígono regular como otro cualquiera pero tiene mil lados, por lo que apenas es distinguible de un círculo.
Sus ángulos internos miden 179,64° grados, con poca diferencia de los 180° de un ángulo llano. Es tan parecido a un círculo que si se calcula su área (sumando los mil delgados triángulos que lo componen) la diferencia respecto al área del círculo sería de menos de un 0,0004% (4 partes por millón).
El chiliágono lo empleó el mismísimo René Descartes allá por el siglo XVII en sus disquisiciones filosóficos. Así que también tiene su «historia» como ejemplo de algo que «parece pero no es», de una «representación confusa de la realidad» y otras sutilezas por el estilo.
Pero ¿por qué pararse en 1.000 lados? Encontré que más allá del chiliágono están el miriágono (10.000 lados) y el megágono, que tiene un millón de lados, con ángulos internos de 179,99964°. Incluso si esta absoluta megabestia de la geometría mental se dibujara con sumo cuidado alrededor de la superficie de la Tierra seguirá sin distinguirse de un círculo: la diferencia serían unos 0,0625 milímetros, lo cual obviamente no es nada comparado con el círculo máximo del ecuador terrestre, que mide unos 40.000 kilómetros.
Una curiosidad es que el chiliágono se puede construir «con regla y compás» siguiendo las reglas de los polígonos construibles, debido a las características de los factores divisores de 1.000. En cambio el megágono no puede ser construido por este método, como les sucede a los polígonos regulares de 7 y 9 lados, entre muchos otros.
(Vía @Pickover.)


