Karl Sims tiene una página a la antigua usanza explica de forma sencilla y visualmente qué son y cómo se construyen los conjuntos de Julia y de Mandelbrot, dos de los fractales más conocidos e íntimamente relacionados. Los detalles en Understanding Julia and Mandelbrot Sets.
Estos conjuntos aparecen a partir de funciones muy simples como zn+1 = zn² + c en donde c es un número imaginario. Al utilizar el resultado de la fórmula (empezando por z0 = z) como nuevo valor de entrada y repetir la operación una y otra vez se obtiene una sucesión. Para algunos valores ese resultado está dentro del conjunto (valores menores que 2) y para otros, fuera (infinito).
Se puede crear un gráfico de píxeles con todos estos valores. Los que están fuera se suelen colorear según la «velocidad de divergencia» con la que tienden al infinito; de esta forma surgen bellas y coloridas formas con el clásico toque fractal y la característica autosemejanza – que puede observarse si se utilizan diferentes valores iniciales con más y más decimales («ampliación»). Las fórmulas y algoritmos del conjunto de Mandelbrot son muy similares a las del de Julia, por eso aunque se ven diferentes están tan relacionados.
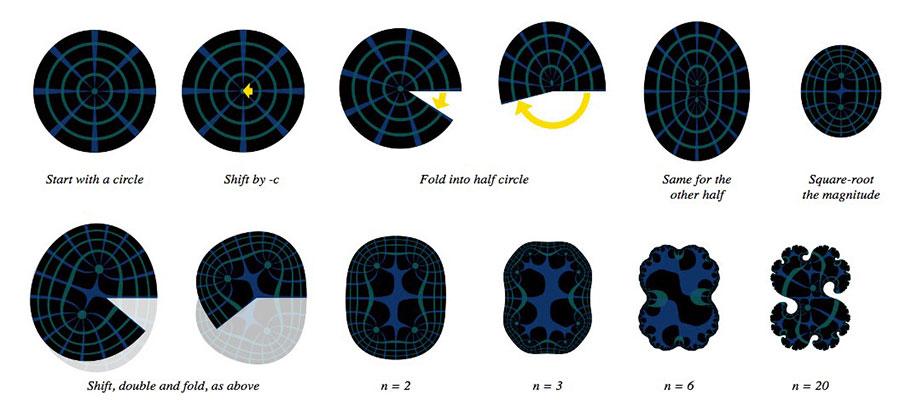
La imagen de la página original muestra visualmente cómo son las transformaciones y de dónde surge su complejidad: del «efecto de doblar y estirar», como con los fideos chinos o cuando se mezclan los naipes de una baraja.
El vídeo que muestra el proceso ayuda a entender también por qué variar incluso una ínfima fracción decimal los valores iniciales da lugar a formas tan complejas y distintas: porque el efecto de la potenciación repetido una y otra vez tiende a «separar» todos los puntos, aunque originalmente estuvieran muy cerca unos de otros.
Relacionado:
- El caso de los fractales desaparecidos
- Las intrincadas dimensiones de los fractales y la autosemejanza
- Juegos caóticos y fractales
- Fractales fractales y otras visualizaciones autorreferentes
- Los sonidos del conjunto de Mandelbrot
- Curvas para rellenar el plano y el espacio
- Buddhabrot: un fractal nebuloso animado en colores a 4K