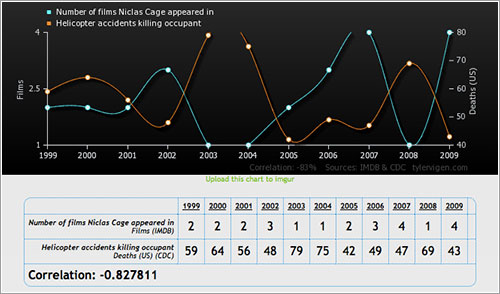
En azul, las películas en las que sale Nicolas Cage; en rojo los accidentes de helicóptero con víctimas mortales. La correlación es de -0,827811, bastante buena
Spurious Correlations es un blog en el que se demuestra que si torturas los datos lo suficiente, estos te dirán lo que quieras.
En concreto, se dedica a estudiar las correlaciones entre conjuntos de datos obviamente dispares, y algunas de ellas son muy buenas, muy cercanas a 1 o a -1.
La idea es insistir en aquello de que correlación no implica causalidad; que el que dos hechos estén estadísticamente relacionados no quiere decir que uno sea causa del otro.
Como dicen en Nic Cage Prevents Helicopter Accidents, Or Why Correlation Does Not Mean Causation, para que haya causalidad tienen que darse al menos:
- Una correlación, de tal forma que si queremos decir que X ha causado Y entonces X tiene que estar correlacionado con Y.
- Un orden temporal, de tal forma que si X causa Y no puede ser que Y cause X; algo tiene que pasar primero y provocar un cambio. Hay que tener cuidado además con aquello del Post hoc ergo propter hoc, pues no siempre el que algo pase después de otra cosa implica que la primera sea causa de la segunda.
- Que no haya otras variables que influyan; si tienes los puntos 1 y 2 de esta lista tienes que asegurarte de que no hay nada por ahí oculto que esté influyendo en el resultado.
El problema es que es relativamente sencillo encontrar dos conjuntos de datos que cumplan el primero de estos puntos y que muchas veces olvidamos que con eso no basta.
Aparte de los casos ya presentados, en el sitio se pueden crear otros gráficos haciendo clic en los nombres de los conjuntos de datos.



