La coincidencia de «Los cuatro cuatros» explica cómo obtener todos los números del cero al diez utilizando siempre cuatro números cuatro y diversas operaciones matemáticas básicas. Por ejemplo 7 = (44/4)-4. Es curioso que en el libro original del que está extraída esta curiosidad, El hombre que calculaba, la explicación esté en la página 44.
Actualización: Marcelo nos contó por correo que además de los números del 1 al 10 se puede llegar a escribir cualquier número con cuatro cuatros, mediante esta increíble fórmula:
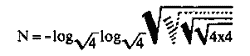
El ejercicio mental de ir obteniendo sin esta fórmula todos los números hastas el cien con sólo cuatro cuatros es apasionante. A partir del 19 algunos requieren usar factoriales, a veces un truco de expresión anglosajona usando .4 para referirse 0,4 o también los signos para «parte entera del número», o una combinación de todo lo anterior. El hecho de que la raíz cuadrada de 4 sea 2 ayuda bastante. Todo esto lo cuenta el mítico Jaime Poniachik en la sección Trotajuegos de la revista Juegos para la Mente (hermana mayor de la no menos legendaria Cacumen) en los años 80, de la que se puede accederse a esta versión escaneada que nos mandó Marcelo: Breve visita a los cuatro cuatros [GIF, 64 KB]. (Nota: en el original a la fórmula anterior le falta un signo menos, que he corregido aquí.)
(Vía ThE FuCkInG sHiT.OrG.)
- Reloj 9, una forma simpática de cómo obtener los números del 1 al 12 utilizando siempre tres nueves.


