Que el valor del número pi (π) se conoce desde la antigüedad –al menos desde el año 1800 o incluso 2000 a. C.–es un hecho cierto. Por suerte también han llegado hasta nosotros los métodos que hace miles de años se emplearon para realizar los cálculos de su valor aproximado. Algo interesante, dado que hasta pasados muchos siglos (en el siglo XVIII) no se obtuvo una demostración de que el valor de pi era irracional, es decir que no era un valor que pudiera expresarse como una fracción.
Uno de los métodos más conocidos por ingenioso es el de Arquímedes de Siracusa en Los elementos. Hay una traducción paso a paso aquí: Archimedes’ Approximation of Pi. Y en Math Scholar hay también otro largo artículo que amplía la idea original: Simple proofs: Archimedes’ calculation of pi utilizando algunas técnicas más modernas.
El planteamiento de Arquímedes no era del todo original, dado que se sabía que la longitud de una circunferencia (y por tanto su relación con π) sería muy similar a la longitud de un polígono regular inscrito o cincunscrito a la misma. Cuantos más lados, más preciso sería el valor. La novedad del método de Arquímedes fue que su idea era un proceso iterativo, de modo que repitiéndolo se podían obtener valores de π cada vez más precisos.
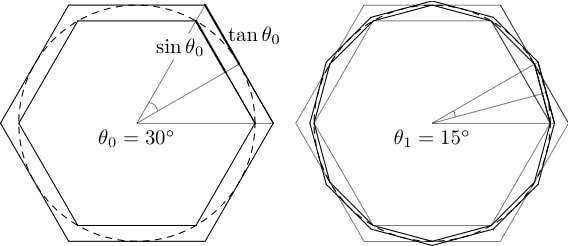
Tampoco se conocen los detalles exactos del método de Arquímedes porque se saltó muchos cálculos, pero más o menos se sabe cómo lo hizo: utilizó un polígono (hexágono) inscrito y otro circunscrito respecto al círculo unidad. El valor de π quedaría por tanto entre ambos perímetros, más grande que el primero, más pequeño que el segundo. Luego repitió el proceso multiplicando por dos el número de lados: 12, 24, 48 y 96, con lo que se lograba cada vez más precisión. Curiosamente al hacer esto estaba eliminando en cierto modo la geometría y convirtiéndolo todo en un procedimiento meramente aritmético.
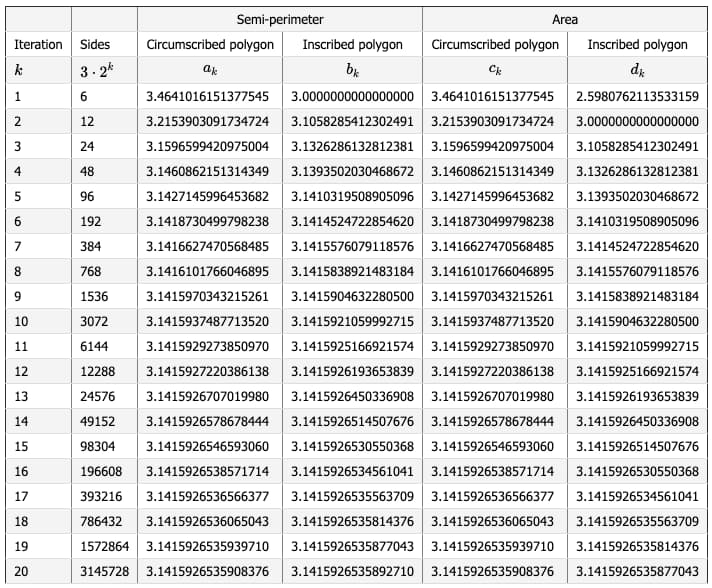
Hoy en día podemos poner las calculadoras a trabajar y sin mucho esfuerzo iterar el cálculo 20 veces, lo cual produce polígonos de 3.145.728 lados y un valor de π de 3,1415926535… en el que ambos polígonos coinciden hasta el décimo dígito decimal. Arquímedes se quedó en:
polígono de 96 lados: 3 10⁄71 > π > 3 1⁄7
{Imagen: Michele Vallisneri, NASA JPL}
Relacionado:
- El descubrimiento del valor de pi
- Cómo calcular el valor de π por diferentes métodos
- Los seis primeros libros de los Elementos de Euclides con gráficos modernizados de Oliver Byrne, disponibles en línea
- Los Elementos de Euclides, modernizados tanto en texto como en estilo
- La evolución de Pi con el tiempo
- Mechanical pi, o cómo calcular π de una forma especial
- ¿Para qué sirve conocer o calcular millones y millones de dígitos de π?
- Estudiantes del MIT escribiendo π
- Usos práctico de los decimales de pi
- Pi Trainer, para entrenarse en memorizar π