Por @Alvy — 18 de Mayo de 2010
Para malabarismos matemáticos raros, nadie mejor que la gente de Futility Closet y sus lectores. Uno de ellos (Robin) les envió estas aproximaciones a π y e obtenidas en operaciones aritméticas sencillas donde participan todos los dígitos del 1 al 9 (además de los paréntesis y la coma/punto decimal cuando es necesario):
π con diez decimales, descubierto por B. Ziv en 2004:
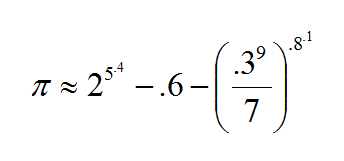
e con 18 cuatrillones de decimales correctos (¡tiene mérito!) descubierto por Richard Sabey en 2004.
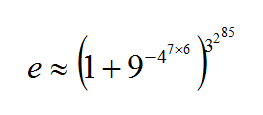
Lo de que la segunda aproximación, tan aparentemente simple, tenga cuatrillones de decimales correctos y luego sea ligeramente distinta de e me tiene fascinado.
Actualización (19 de mayo de 2010): Tal y como nos explicaron por correo GNRS y Miquel:
La aproximación a e es tan precisa debido a que e se define como el límite cuando n tiende a infinito de (1+1/n)n. En este caso, n=3(285), que es un número enorme y por consiguiente coinciden muchísimos decimales. El mérito es expresar n y 1/n con los dígitos del 2 a 9 (el 1 del principio que está sumando no puede cambiarse).
