Connor Flood ha sido el encargado de un proyecto apasionante en las tripas de Wolfram Alpha, ese poco conocido «motor de conocimiento» con aspecto de buscador pero que cuenta con gigantescas bases de datos estructuradas y con el cerebro de Mathematica, el software de computación simbólico. El resultado es que ahora permite generar pruebas matemáticas mediante inducción a partir de una consulta en lenguaje normal y corriente.
Los detalles tecnico-matemáticos son bastante complejos pero baste saber que la respuesta a las demostraciones que se solicitan no son básicamente resultados como «cierto» o «falso», sino el «paso a paso» que lleva de la proposición a la demostración.
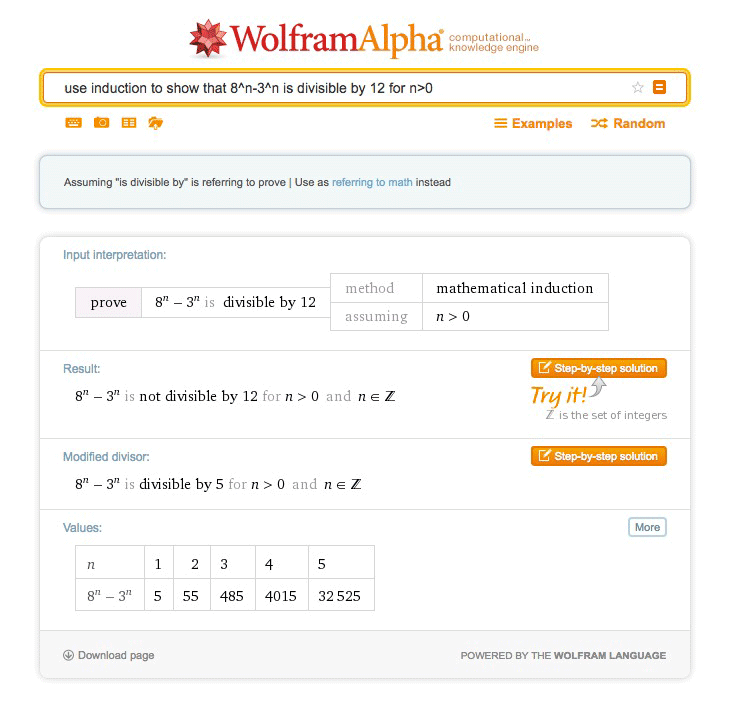
Un ejemplo típico sería
Demostrar que 8 elevado a n menos 3 elevado a n es divisible por 5 para cualquier valor de n mayor que 0.
Puede comprobarse con lápiz y papel que la afirmación es cierta para muchos valores de n, pero lo complicado es demostrarlo para todos los valores que se indican. El programa puede demostrar igualdades, desigualdades o cuestiones de divisibilidad.
Se suele explicar lo que es la inducción matemática comparándola con el «efecto dominó»: si le sucede algo a una primera ficha y se puede demostrar que eso hace que le suceda algo a la inmediatamente siguiente entonces el resto irán cayendo una tras otra, dentro de los límites que se establezcan. Matemáticamente se establece primero la base de la demostración y se demuestra el primer caso para luego hacer lo mismo para el siguiente paso inductivo, que permite generalizar la hipótesis.
Se pueden leer más detalles sobre cómo se ha diseñado este motor de demostraciones en el artículo de su creador: Behind Wolfram Alpha’s Mathematical Induction-Based Proof Generator.
Para probarlo tan solo hay que ir a Wolfram Alpha y escribir alguna expresión en con la sintaxis adecuada, que es además muy flexible.


