Todo el mundo ha oído hablar de un modo u otro de la Distribución de Pareto, de la «regla del 80-20» o el principio de Pareto y aquello de que en muchos ámbitos cuando una población o actos contribuyen a un «efecto común» suele suceder que una proporción pequeña es la que contribuye a la mayor parte del efecto. Está relacionada con la ley de Bradford y en este ejemplo con la curva de Lorenz, que se lee como un porcentaje acumulativo.
Para analizar este tipo de datos Felipe Hoffa ha publicado un artículo titulado Inequality: How to plot a Lorenz curve with SQL, BigQuery, and Data Studio donde explica cómo aplicar este tipo de análisis utilizando una combinación de herramientas. Es un poco técnico pero interesante y con suficientes enlaces como para aprender e investigar más al respecto.
Como conjunto de datos de ejemplo Hoffa ha utilizado los datos de audiencia de la Wikipedia, que son públicos. La enciclopedia libre recientemente ha llegado a los 6 millones de artículos publicados en inglés. Cada una de esos millones de páginas individuales recibe más o menos visitas a lo largo del día, contribuyendo de este modo de forma común a una audiencia total realmente masiva (#13 del mundo actualmente, según Alexa.)
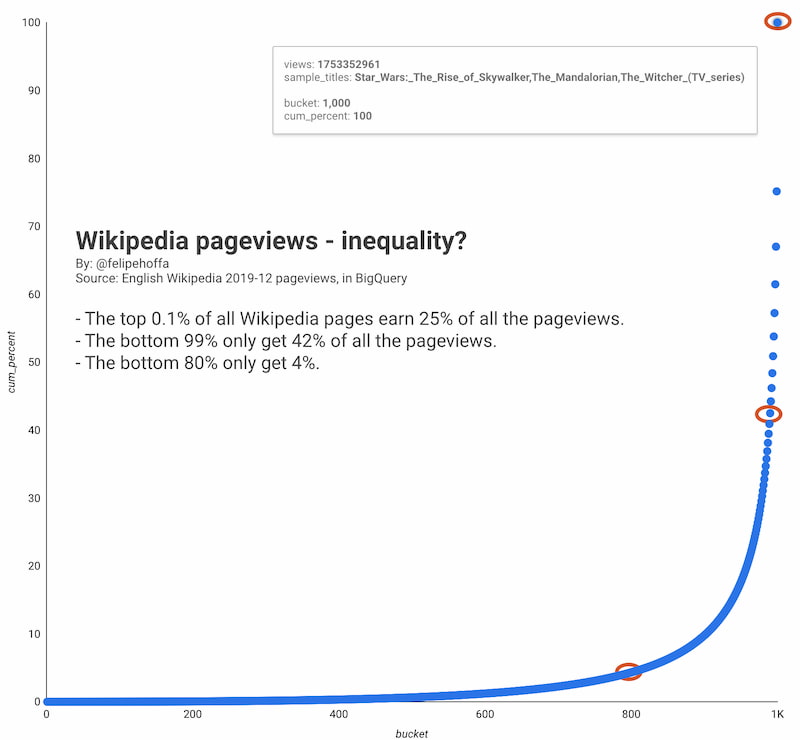
Pero aquí viene la «gracia» del asunto: si se hace una gráfica de la curva de Lorenz, se ve claramente la «desigualdad» de esos contenidos. El 0,1% más popular de los artículos de la Wikipedia acumula el 25% de las consultas, mientras que el 80% menos popular sólo totaliza el 4%. De hecho al 99% que queda fuera del «top 1%» sólo llegan el 42% de las visitas. Viendo el Top 50 Report (2019) es fácil hacerse una idea de a qué se debe esa «popularidad»:
Excepto la lista de «fallecidos por años» –un clásico de consulta– el resto es una combinación de contenidos populares del cine y la televisión, con Los vengadores a la cabeza y los eventos y personajes reales en los que están basados documentales (Ted Bundy), películas (Freddie Mercury) y series (Chernobyl) a continuación.
Hay quien pensará que quizá sea un poco desigual o incluso injusto que entre 6 millones de páginas sobre el conocimiento humano este tipo de contenidos acaparen tanta atención, pero es lo que hay. Hace más de una década reflexionábamos acerca de por qué «Britney Spears» rompía récords de búsqueda en Internet y las cosas no parecen haber cambiado mucho.
Relacionado: