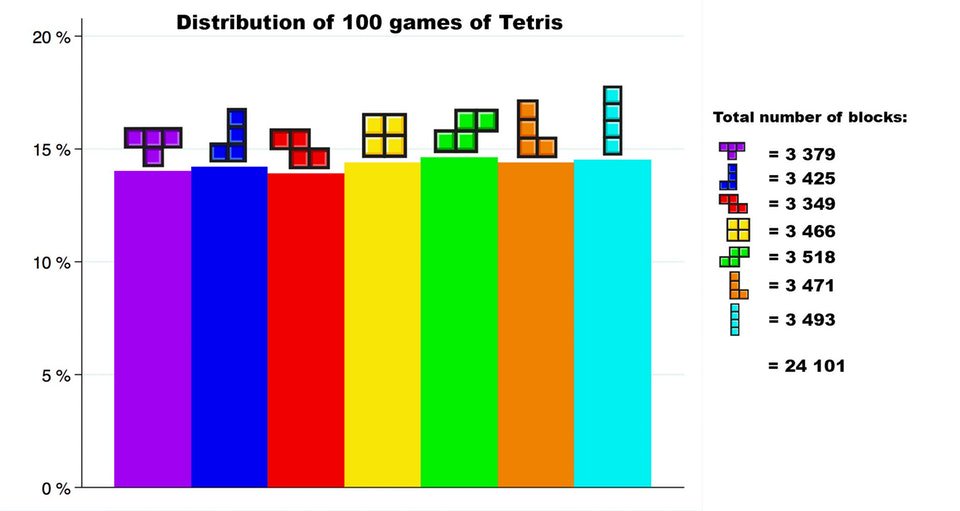
Mezvan compartió hace un tiempo esta imagen de la distribución de piezas en una partida de Tetris, un tanto chocante porque contiene más piezas largas –llamadas «I» por su forma– de lo que se suele experimentar. Así que estuvimos mirando algunas páginas al respecto.
Resulta que el algoritmo generador de piezas aleatorias del Tetris no es tan trivial como se podría pensar. Si aparecieran piezas puramente al azar cada una de ellas tendría 1 probabilidad entre 7 de ser la siguiente. Pero esto podría llevar a series demasiado repetitivas y que en caso de tener «muy mala suerte» que no apareciera la pieza deseada en una larga secuencia quizá de 10, 20 o 40 piezas (suficiente como para matar la partida). Así que sus creadores pensaron en otras fórmulas.
Según parece el «generador de piezas» –que es como lo llaman– varía de unas versiones del juego a otro. En el Tetris de Gameboy por ejemplo se intentó que la misma pieza no pudiera aparecer tres veces seguidas. Cada pieza tiene asignado un código binario entre 000 y 110 y se realizan diversas operaciones OR con un valor al azar dependiendo de los dígitos anteriores, rechazando las nuevas piezas generadas si no cumplen «ciertas condiciones». El resultado de esa complicación es que en la práctica las probabilidades son: L: 10,7%; J, I, Z: 13,7%; O, S, T: 16,1%. (Ese algoritmo es de Henk Rogers).
Tal y como explican en el Tetris Wiki, la versión más «oficial» al respecto dice que su generador aleatorio funciona considerando las siete piezas (I, J, L, O, S, T, Z) mezclándolas como si fueran una baraja de naipes y sirviéndolas por orden como «sacándolas de una bolsa». En total hay 5.040 permutaciones posibles, de modo que a una mezcla de las primeras siete pueden seguir unas ~5.040 mezclas distintas a continuación y es difícil que se repitan completas. La distancia más larga entre piezas iguales tiene 12 piezas intermedias (por ejemplo siendo la primera una I y la última otra I, con otras 12 entre medias). Pero hay variantes de este algoritmo que emplean «bolsas» de 8 piezas, con una de ellas repetidas, y otros en los que la primera pieza de cada bolsa siempre ha de ser I, J, L o T.
Colateralmente Mezvan nos pasó también el enlace a Playing Tetris forever donde se explican los algoritmos para «jugar eternamente al Tetris», métodos que tienen algunas limitaciones (como que el generador aleatorio tenga ciertas características y se conozcan las tres piezas «siguientes», cosa que no sucede en todas las versiones) pero que resulta muy interesante también.