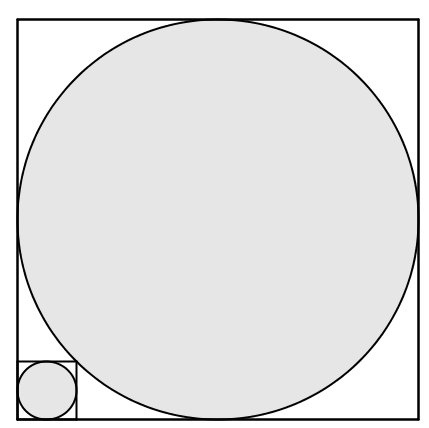
Si el radio del círculo grande vale 1, ¿cuál es el área del círculo pequeño?
En Solve My Maths suelen plantear muchos problemas geométricos de este estilo, que son fáciles de entender y no tan fáciles de resolver – combinación ideal.
En este caso preguntaron sobre una composición con círculos, cuadrados y un área. Hay que dar por supuesto que no hay truqui y son círculos tangentes con los cuadrados, con los puntos de contacto en los lugares obvios. Pista: resolviendo paso a paso con lo que se sabe se va averiguando lo que no se sabe. ¡Y no olvides leer dos veces la pregunta!
La respuesta no requiere de grandes cálculos, pero tampoco es obvia ni de esas que se puedan hacer de cabeza – aunque no estará fuera del alcance de mucha gente, y supone un reto mayor.
La solución en este enlace y en este hilo – pero ojo que muchísima gente ha dado respuestas incorrectas.
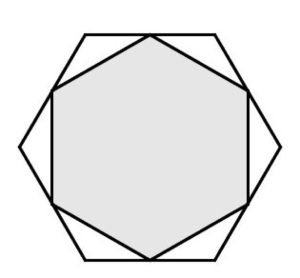
Bonus: Si te ha parecido fácil, prueba a calcular qué fracción del área del hexágono grande está sombrada sabiendo que su área es el hexágono inscrito más pequeño.
(Vía @Pickover.)
Relacionado:
- Un problema geométrico sobre el envoltorio de un cubo con papel
- Círculos: cuestión de geometría
- Cómo resolver problemas geométricos con programas informáticos
- Los 150 problemas matemáticos de Nick
- El problema de los tres triángulos
- Euclides, el juego: una forma lúdica de repasar (o aprender) geometría
- La ciudad de Königsberg, sus siete puentes y la teoría de grafos
- Los ángulos de un triángulo suman 180 grados: demostración
- MathCaching
- El burro y la alfalfa