La forma en la que las matemáticas resuelven los problemas del MundoReal™ suele pasar por crear «modelos» con los que realizamos cálculos partiendo de ciertas suposiciones. Mejorando esos modelos con nuevos detalles y variables esas soluciones tienen en cuenta más factores y resultan más precisas. Un físico, un ingeniero o una persona sin conocimientos específicos probablemente tiraría por el camino más rápido, haría una medición y listo.
Este trabajo de Peter Johnston titulado How long is my toilet roll? – a simple exercise in mathematical modelling escenifica precisamente esa situación de forma seria pero a la vez entretenida, algo digno de ser enseñado en clase. Se trata de algo tan simple como calcular la longitud total del papel de un rollo de papel higiénico.
Fórmula tras fórmula
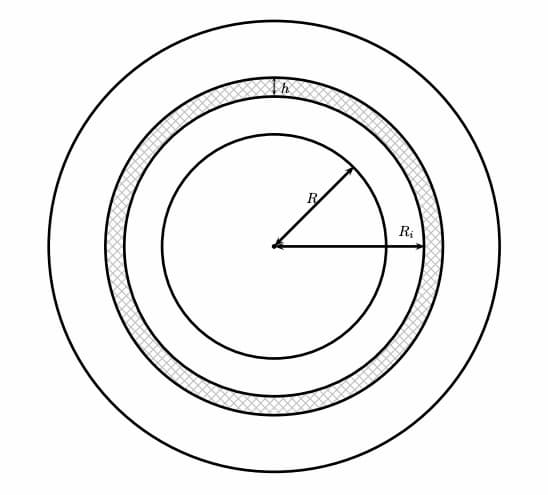
El trabajo explica los diferentes modelos: primero se puede suponer que conociendo el diámetro del cilindro de cartón central (R) y el grosor de la zona de papel (D) junto con su espesor (h) sería suficiente: podemos imaginar que hay n = D/h vueltas de papel, que varían entre 2πR y 2π(R+D) y hacer el cálculo con un sumatorio.
Pero sabemos que el rollo no son círculos perfectamente concéntricos, sino más bien una larga espiral, así que el cálculo se quedaría algo corto. Otra aproximación sería promediar los radios de cada vuelta con la siguiente, y sería algo más preciso. Esto se resuelve con otro sumatorio. La fórmula resultante:
2πRn + πn2h
Finalmente está la solución más precisa, que es darse cuenta de que en realidad la gran hoja de papel forma una espiral, cuya distancia al centro del rollo depende del ángulo. Más exactamente es una espiral de Arquímedes con una distancia fija entre cada capa a cada vuelta. El resultado más simple es una fórmula que ya «asusta» un poco más:
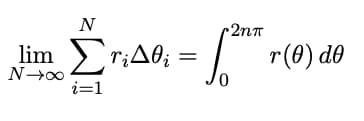
Curiosamente, si se simplifica resulta que esta fórmula es exactamente la misma que en el caso anterior (2πRn + πn2h). Esto quiere decir que la solución de «promediar» cuando se sabía que la primera fórmula se quedaba un poco corta con otra variable que iba un poco larga ha resultado ser apropiada.
La fórmula «exacta» realizando los cálculos precisos de las longitudes de arco con coordenadas polares (hay otras formas de calcularlo de forma aproximada) es llamativa; más que nada por lo grande que resulta, aunque es bastante simple sustituyendo las variables por sus valores:
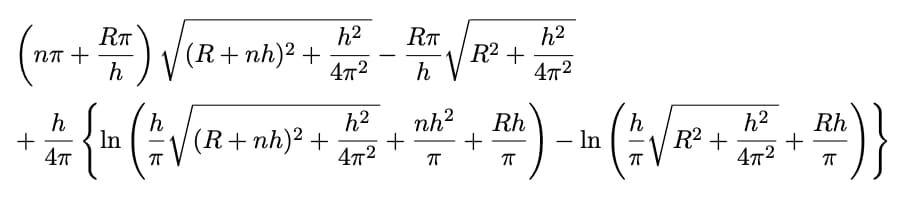
De vuelta al MundoReal™
Pero lo más divertido de todo es que en el MundoReal™ esto no funciona del todo bien. ¿Cómo lo sabemos? Johnston fue a la tienda y compró un rollo. Lo midió obteniendo 55 mm de radio interior (R) y 20 mm de ancho de la zona del papel (D); después con una herramienta de precisión calculó el grosor de las capas (h) que eran de 0,36 mm (aquí tuvo que promediar). Según la primera fórmula el papel debía medir 22.797 mm, según el segundo y tercer método, 22.907 mm; el cuarto método también daba 22.907 mm aunque con una pequeña diferencia en el segundo decimal. Pero al desplegar y medir el rollo se encontró con que medía 23.200 mm, casi 30 cm más de lo previsto. El error había sido de aproximadamente del 1,5 por ciento.
El ejercicio completo es todo un precioso trabajo sobre cómo crear un modelo, mejorarlo, calcular, seguir calculando y luego comprobar hasta qué punto es correcto o no gracias a la experimentación. Ciencia pura. También de que las cosas en el MundoReal™ son medibles pero hay ciertos factores imponderables, incógnitas y errores de precisión en las herramientas de trabajo que hacen que la labor de físicos, ingenieros y quienes trabajan «sobre el terreno» tenga tanto valor como el de las matemáticas teóricas e ideales.
Relacionado:
- ¿Para qué sirve calcular millones y millones de dígitos de π?
- Corriendo bajo la lluvia
- El valor de pi como «solución inesperada» a un problema matemático
- La constante de aparcamiento de Rényi: ~0,75 coches por coche teórico
- El burro y la alfalfa
(Vía @Pickover)