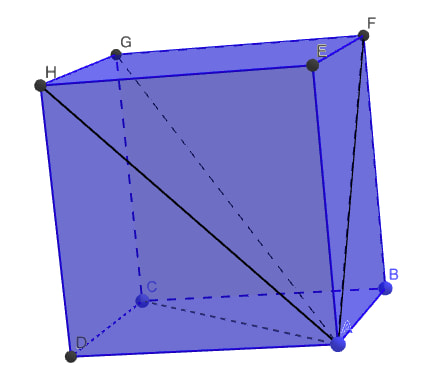
El cuboide perfecto es un ortoedro («caja» o «ladrillo») cuyas aristas, las diagonales de sus caras y también la diagonal interior son todas números enteros. Es un problema fácil de entender, muy «de Pitágoras». De hecho su famosa fórmula a²+b²=c² es parte del problema… y de la solución, claro. Si existen los «rectángulos perfectos» (por ejemplo el de aristas 3 y 4 con diagonal 5). ¿Por qué no también los «cuboides perfectos»?
El problema es que a día de hoy no se conoce ninguno.
Una versión más sencilla del cuboide perfecto es el ladrillo de Euler, donde todas las aristas y diagonales son enteras, excepto la interior. Probablemente es un problema que viene incluso de antes de Euler; la primera solución que se conoce es de Paul Halcke (en 1719) con aristas (44, 117, 240) y diagonales (125, 244, 267). Se sabe que existen infinitas soluciones. Al cuboide perfecto también se le llama «ladrillo de Euler perfecto» o «caja racional».
Aunque los matemáticos han estado intentando encontrar un cuboide perfecto desde hace siglos –o demostrar que no existen–, todavía nadie ha dado con uno, ni siquiera mediante búsquedas informáticas exhaustivas, un método un poco de «fuerza bruta» al que a veces se recurre ante la desesperación.
Curiosamente, se saben muchas cosas descorazonadoras sobre esa posible solución: de existir la arista más pequeña debería ser mayor que 5×1011, alguna arista, diagonal o diagonal interior debería ser divisible por 37, y la diagonal interior no sería una potencia principal ni un producto de dos primos. Entre otras muchas cosas.
Aquí dejo algunos enlaces a trabajos y artículos para saber más sobre el tema:
- Perfect Cuboid en MathWorld
- The surface parametrizing cuboids, Michael Stoll y Damiano Testa
- On Perfect Cuboids, Ronald van Luijk
- La caja de Euler, Gaussianos
- Ladrillo de Euler, Wikipedia
- Euler Brick, Wikipedia
Se considera uno de esos problemas muy fáciles de entender, incluso para quienes no sepan mucho de matemáticas, pero sumamente difícil de resolver. Fama y gloria eterna para quien encuentre una solución.
Relacionado: