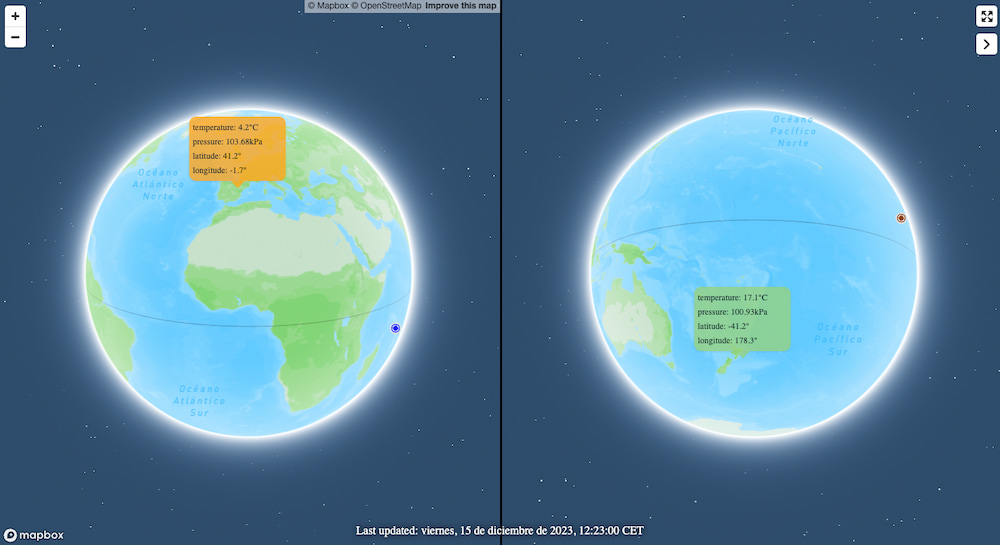
Cotter y Ross presentan una curiosa página en la que se puede explorar el teorema de Borsuk-Ulam interactuando con un ratón sobre un mapa del mundo. O, más exactamente, dos mapas: el de un punto sobre el globo terráqueo y el de sus antípodas. ¿Es posible encontrar dos puntos en la Tierra donde la presión atmosférica y la temperatura sean exactamente iguales en un momento dado?
La respuesta es que sí. Siempre se puede.
¿Y qué dice al respecto el Teorema de Borsuk-Ulam? Es una de esas intrigantes cuestiones matemáticas que apuntan a algo poco intuitivo: que las medidas de este tipo, al ser continuas, poseen esta propiedad en puntos antipodales. Además, dado que un mapa del mundo sobre un globo terráqueo es bidimensional, el teorema «funciona» con dos variables simultáneamente.
Karol Borsuk y Stanislaw Ulam demostraron este teorema en la década de 1930, y aún se enseña como un concepto fundamental en topología. Resulta interesante que actualmente se pueda visualizar de forma tan clara e intuitiva en un mapa, dado que su explicación mediante ecuaciones es mucho menos evidente.
Relacionado: