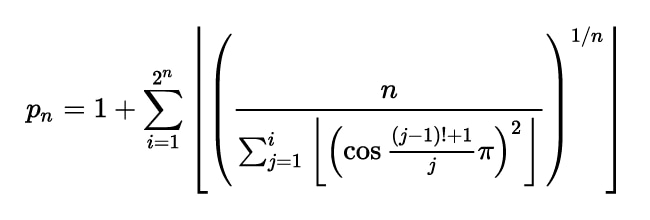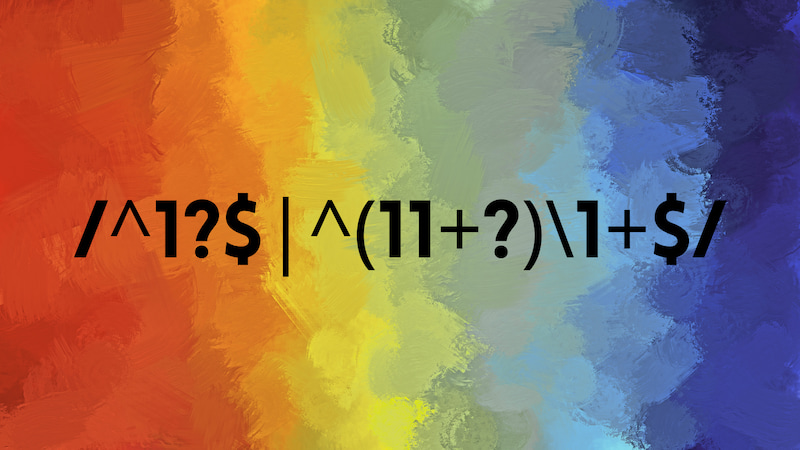Dos curiosidades sobre fórmulas relacionadas con los números primos

Por @Alvy — 18 de Agosto de 2023

Esta regexp en Perl comprueba si un número es primo o no / Avinash Meetoo

En los últimos meses descubrí un par de curiosidades sobre fórmulas para generar números primos y comprobarlos, entendiendo por «fórmulas» o bien una función matemática o bien un programa sencillo que genera todos los números primos o que comprueba su primalidad.

Ya hace siglos que Euler vio que n² - n + 41 genera toda una serie de números primos… pero sólo entre el 1 y el 40… ¿Sería una serie válida para generar más números primos? Pues no: con n = 41 la fórmula da como resultado 1681 que resulta ser el producto de 41 × 41, algo obvio al examinar la fórmula.

La idea de multiplicar todos los números primos en secuencia y sumarles 1 tampoco sirve. Veamos un ejemplo:

2 × 3 × 5 × 7 × 11 × 13 + 1 = 30031

pero resulta que 30031 = 59 × 509. La idea deja de ser válida porque la multiplicación crece muy rápido y puede tener factores primos por encima de los que se están multiplicando, algo que no se ha tenido en cuenta en la idea original.

La fórmula para generar primos de C.P. Willans

¿Es posible que exista una fórmula para generar todos los números primos por su orden? Siempre había oído que teóricamente no existen, y que encontrar «el siguiente número primo» es laborioso. Pero resulta que sí que existen… aunque su utilidad como se explica más adelante es bastante discutible. Véase:

Esta es la curiosa fórmula que C.P. Willams publicó en 1964. No es muy complicada de interpretar: el enésimo número primo (p_n) es 1 + un sumatorio entre 1 y 2ⁿ de una fracción que incluye otro sumatorio con un factorial, un coseno y el número π (¡toma ya!). Se toma el valor absoluto, se hacen unas potencias, una división, alguna cosa más y ¡voilà! Enésimo primo listo.

El caso es que es fácil probar incluso manualmente algunos valores pequeños, o programar la fórmula en el ordenador y darle valores para observar cómo con el 4 genera el 4º número primo (7), o con el 10 el 10º número primo (29). ¿Qué brujería es esta?

Hay un vídeo estupendo de Eric Rowland que desglosa cuidadosamente el «funcionamiento» de la fórmula paso a paso para explicar cómo una parte se comporta como «detector de números primos»:

El sumatorio funciona como un bucle entre 1 y el número a probar (el 1+ del principio sirve para que el primer primo sea el 2). Al ir recorriendo la secuencia de los números naturales devuelve valores 0 ó 1 si el número es primo o no, y en cuyo caso se «anula» ese término para pasar al siguiente, simplemente porque el valor es cero. Si el bucle se completa es que el número realmente es primo, y se puede dar por bueno. El coseno y π se utilizan virtuosamente para hacer que ciertos valores de comprobación varíen entre -1 y 1 con distintos significados*.

Pero, ¿cómo sabe si un número dado es primo? El algoritmo viene a funcionar verificando por orden todos los números naturales y respondiendo en bucle a preguntas como «Es el número de primos hasta 2 menor que 4?» «Es el número de primos hasta 3 menor que 4?» y así sucesivamente para valores de i, j y n. Muy listo no es.

Es fácil ver que es terriblemente ineficiente: el sumatorio es entre 1 y 2ⁿ, un valor que crece de forma brutalmente exponencial: para 4 hay que comprobar hasta el 16 pero para 100 ya es casi un gúgol; el otro sumatorio para comprobar la primalidad y el factorial empeoran el panorama. Además, cada paso requiere recalcular toda la serie de nuevo, algo bastante absurdo entendido como un «algoritmo», aunque esa era su naturaleza, claro.

Hubo cierto debate sobre la esencia de esta fórmula, que se considera «correcta, pero completamente inútil». No explica de donde surgen los números primos y simplemente los va mirando y enumerando como si lo hiciera un escolar de primaria. Pero acierta. Así que ahí queda.

La expresión regular que genera primos (y en solo 18 caracteres)

Esta regexp (expresión regular) de Perl, que también funciona en Ruby comprueba si un número es primo o no:

/^1?$|^(11+?)\1+$/

¿Puede algo tan escueto factorizar un número y comprobar si es primo o no? Es sabido que las regexp son rebuscadamente crípticas, pero basta ejecutar un programa con un bucle de números naturales y la regexp en cuestión para ver cómo escupe números primos cual oso que caga números primos, sin fallos.

El artículo de Avinash Meetoo destripa la expresión en sus dos partes, antes y después de la barra vertical (|). La primera parte es trivial para eliminar los valores 0 y 1.

La segunda parte es donde está la chicha, que básicamente consiste en que los números se representan como cadenas de unos, de modo que por ejemplo 8 es 11111111 (ojo: no es binario, son 8 unos). La expresión se comporta de forma recursiva, buscando si la cadena es «divisible» por todos los números más bajos, como el 2 (11), el 3 (111), etcétera sin que tras iterar sobre toda la cadena sobre nada. Si todas las pruebas fallan, el número no es divisible (o más bien «troceable») por ninguno más pequeño, de modo que es primo y se muestra como tal.

Este método también es tremendamente lento, e incluso en ordenadores modernos más allá de 1 millón se ejecuta a velocidad de tortuga, pero funcionar, funciona.

Hay más detalles y alguna que otra curiosidad extra en el foro de Hacker News donde Meetoo envió su idea, incluyendo versiones similares en otros lenguajes y el debate sobre cuán válidas (o faltas de practicidad) son estos ingeniosos pero inútiles algoritmos.

_____
* Este método de usar trigonometría, valores absolutos y sumatorios a modo de bucles tiene muchas aplicaciones en otros algoritmos informáticos, si se puede hacer de forma eficiente; es una especie de conversión analógica-digital de valores muy distintos a binarios (sí/no) bastante curiosa.

Relacionado: