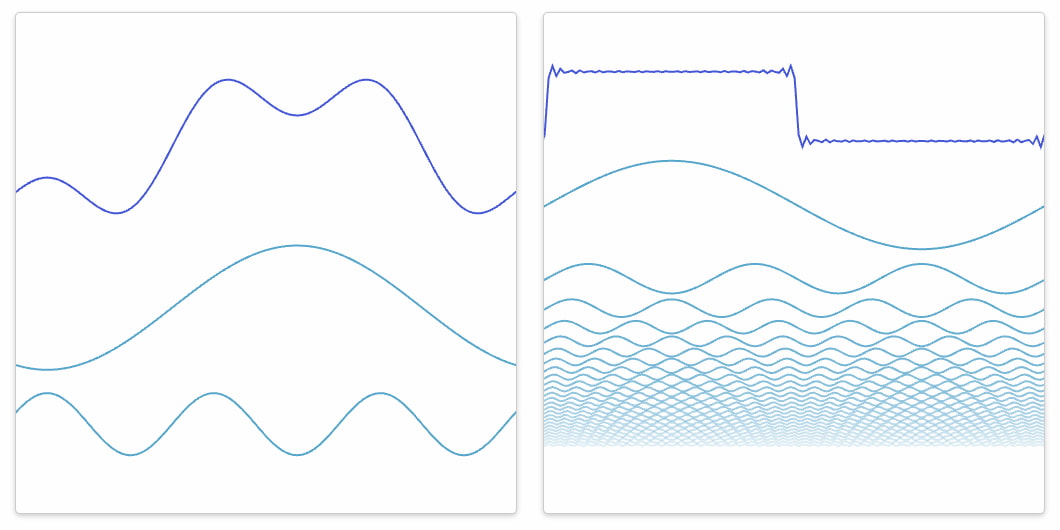
Resulta interesante que en An Interactive Introduction to Fourier Transforms, de Jez Swanson, no haya una sola ecuación de la Transformada rápida de Fourier (FFT) pero es que de eso se trata. Es una introducción visual interactiva al algoritmo que se utiliza en todo tipo de aplicaciones de tratamiento digital: análisis de audio, imágenes y señales variadas, tanto en ingeniería como en comunicaciones y otros campos. Una técnica tan potente que debería estar sin duda en el top 10 de las mejores ideas matemáticas de la historia.
En los esquemas que se pueden ver y manipular con el ratón en la pantalla la onda de la señal analizada suele ser la de arriba (azul oscuro) y sus componentes aparecen debajo. La clave del asunto es entender que la combinación de varias señales simples puede generar una señal más compleja. Puede verse con cierto detalle cómo las ondas sinusoidales más sencillas se combinan para regenerar las señales originales, tan complejas como se quiera.
Al final del artículo hay algunos ejemplos curiosos con epiciclos e imágenes vectoriales SVG y JPEG, siendo quizá el JPEG el más conocido y espectacular a la vez. Al respecto ya publicamos sobre cómo funciona la compresión JPEG, una explicación paso a paso y gracias a este artículo de Swanson es más fácil entender precisamente uno de esos pasos.
Relacionado:
- Cómo funciona la compresión JPEG, una explicación paso a paso
- Viaje interactivo a las entrañas de un archivo JPEG
- El algoritmo de compresión JPEG, explicado con imágenes y fórmulas
- Un trasto mecánico de 1897 para calcular transformadas de Fourier
- Un anuncio de época del Analizador de Fourier HP‑5451A
- Matemáticas dinámicas: estupendas visualizaciones de código abierto
- Las ideas matemáticas que más han influido en el curso de la historia
- Ecuaciones coloreadas como alternativa para explicar conceptos
- Rebuscando a E.T. en los datos de los archivos del Instituto SETI
- 17 ecuaciones que cambiaron el mundo