En este vídeo de Numberphile el profesor Kreck explica y demuestra a grandes rasgos uno de esos hechos matemáticos tan llamativos como útiles. Si una mesa está coja tan solo hace falta girarla hasta encontrar el punto en que queda estable. Tampoco hace falta darle muchas vueltas: el giro será de hecho menor que un cuarto de vuelta (90°) y a veces hay incluso varios puntos de estabilidad.
¿Cómo puede ser esto? Veamos: los taburetes de tres patas nunca cojean. La razón es que tienen tres puntos de apoyo, y tres puntos cualesquiera conforman un plano, de modo que los pongas donde los pongas siempre estarán estables. (Otra cosa es que ese plano sea paralelo al suelo, pero no es eso lo que se discute aquí, simplemente que no «cojee»).
Con las sillas y mesas de cuatro patas, en cambio, sucede que a veces por la rugosidad del suelo los cuatro puntos de apoyo no están alineados en el mismo plano –el suelo– de modo que una de ellas queda más alta que las otras y al apoyarse todo se desestabiliza, oscilando de un lado a otro. Pero se puede demostrar que siempre hay una solución para que quede estabilizada, más allá de calzarlas con un papel doblado, claro.
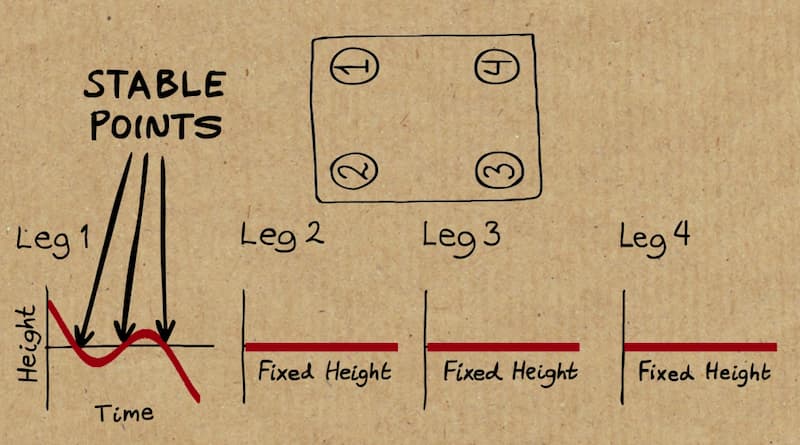
La «razón escondida» es el teorema del valor intermedio que dice que «si una función es continua en un intervalo, entonces toma todos los intermedios comprendidos entre los extremos del intervalo». Considerando la altura de la pata coja respecto al suelo (en un extremo positiva, en otro negativa) en función del ángulo de giro resulta que ha de pasar por el 0 (contacto con el suelo) obligatoriamente.
… Y por eso las mesas de los matemáticos cuando están tomando cervezas en el bar nunca están cojas.
– Profesor Kreck


