Para utilizar este método para hacer raíces cuadradas mentalmente, llamado Método de Herón, sólo hace falta entender cómo funciona el algoritmo –que son tres pasos– y tener cierta capacidad de aproximar un poco la raíz cuadrada y saber hacer divisiones más o menos correctas mentalmente. El tamaño de los números con los que se puede usar depende de la capacidad que tenga cada cual para esos cálculos; de hecho cuanto más altos, más versátil y preciso resulta. La precisión del resultado puede sorprender.
La forma más fácil de entenderlo es un ejemplo; en el artículo de Gregory Gundersen en que lo vi explicado se usa n = 33:
- Se elige un número cuyo cuadrado esté cerca de n (33) por ejemplo g = 6, porque 6×6 = 36.
- Se calcula un segundo número b = n / g, es decir b = 33 / 6 = 5,5 (este cálculo puede ser aproximado, siempre está cerca de g)
- El resultado es la media aritmética entre g y b, es decir (6 + 5,5) / 2 = 5,75.
El valor real de √33 = 5,74456… que no está lejos de 5,75 así que la aproximación es bastante buena, con un error de menos del 0,1%.
Otro ejemplo que probé a hacer mentalmente para verificarlo fue con n = 235. Aquí se puede elegir g = 15. El valor de b lo calculé mentalmente como 15,75 (resulta ser 15,66…) y la raíz calculada sería ~15,37. Realmente la raíz cuadrada de 235 es 15,32…, así que hay solo un 0,3% de diferencia.
Cómo funciona este método de calcular raíces cuadradas mentalmente?
En el artículo de Gundersen se explican todos los detalles, pero básicamente resulta que si la raíz no es exacta, entre el primer valor que se calcula (g) y el segundo (b) el primero sobreestima y el segundo subestima y viceversa. La solución está entre ambos valores y cuando finalmente se calcula la media aritmética ambos valores tienden a compensarse en torno al valor correcto, que está entre ambos.
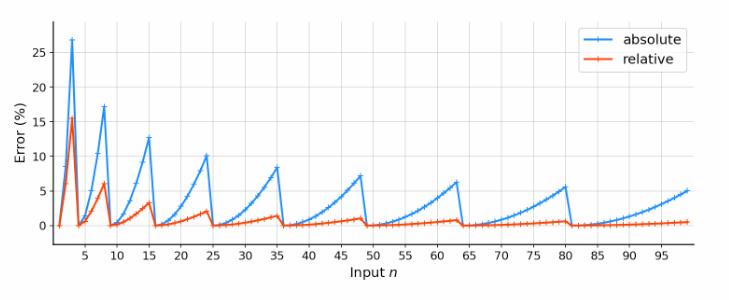
En la gráfica se puede ver los errores absolutos (azul) y relativos (rojo) del método para diversos números, la línea roja marca cero con los cuadrados perfectos, donde no hay error.
Actualización (4 de septiembre de 2023) – Véase Aproximando (muy bien) raíces cuadradas con el método de Herón en Gaussianos, con más detalles matemáticos sobre todo esto.
§
La razón de usar este método mental en vez de la calculadora del móvil, preguntarle a Siri o usar lápiz y papel es que es más complicado y divertido, no hay otra razón práctica – a menos que no tengas nada de eso a mano, te guste hacer ejercicio mental y no vayas a usar los resultados para construir un puente, claro. También está la curiosidad de entender el «porqué funciona» y poco más. Matemáticas especialmente.
§
Me decía el otro día Juanma –un excompi de trabajo que no veía hace casi 20 años– que nos leía menos porque ya no escribíamos artículos de matemáticas :-( Es verdad que últimamente hemos escrito mucho menos sobre esta temática de lo que era habitual en el blog, quizá porque lo tenemos todo muy trillado y casi todo lo que más nos interesaba ya ha sido contado. Pero si nos topamos con algo llamativo seguiremos escribiendo de ello dentro de lo que podamos.
Me permito recordar a todos los lectores que echen de menos ciertos temas o tengan sugerencias para artículos concretos que nos lo digan contactando con nosotros preferiblemente a través de Twitter o correo electrónico, que es lo más rápido.


