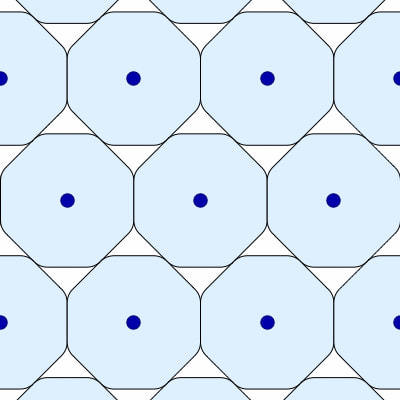
Resulta que el octógono suavizado es la figura geométrica convexa con simetría central con menor densidad de empaquetamiento máxima. O, explicado en palabras más sencillas: si intentas colocar muchos octógonos de estos sobre un plano, la densidad máxima que puedes lograr (entre el área cubierta por las figuras y la superficie total) es ~0,902414, como en el dibujo. En el caso de los círculos, que intuitivamente parecerían las figuras con menor densidad máxima porque desperdician más espacio alrededor, es de ~ 0,906899, un pelín más.
Esta curiosidad es relevante cuando se estudian los llamados problemas de empaquetamiento, que en el mundo real se convierten en cuestiones tales como la mejor forma de aprovechar los troqueles de figuras iguales en una hoja de papel o una lámina de aluminio o cómo meter más naranjas en una caja (en este caso, en tres dimensiones).
Cuando vi el problema me entró una duda, ¿no puede haber distintos tipos de octógonos suavizados? Y así es: dependiendo del radio de suavizamiento o redondez, estos octógonos pueden tener distintas formas, lo cual podría afectar al problema y a su solución. Esto se resuelve aclarando que el octógono redondeado en cuestión es el que tiene un circunradio √2 con el centro en el punto (2+√2, 0) y un vértice en el punto (2,0). Hay algunas ecuaciones respecto a esta construcción, pero en la página de la Wikipedia se puede ver cómo se genera gráficamente, simplemente ajustando la curvatura de tres octógonos regulares hasta que forman un triángulo.
Esta curiosa forma geométrica dio lugar a la llamada conjetura de Reinhardt que afirma que este tipo de octógono redondeado es efectivamente la figura convexa con simetría central de mínima densidad de empaquetamiento máxima, aunque todavía no se ha podido demostrar. Se considera un relevante problema no resuelto en matemáticas, que no acarreará seguramente ningún premio para quien consiga una demostración pero sí algo de fama y gloria.
(Vía @RobinHouston.)