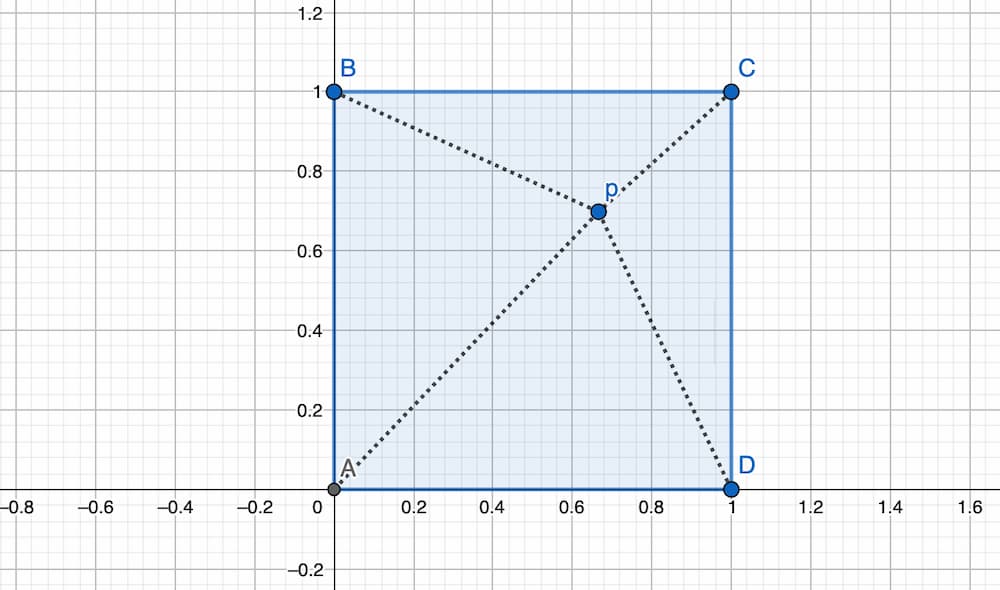
¿Existe un punto en el cuadrado unidad cuya distancia a cada una de las cuatro esquinas sea un número racional?
Según parece todo apunta a que respuesta es que no, pero no se conoce todavía una demostración.
Se trataría de encontrar un punto en cualquier lugar del interior cuyas distancias fueran expresables como una fracción, pero no parece fácil. John Conway y Richard Guy encontraron algunos puntos con tres distancias racionales, pero no con cuatro. Se ha demostrado que si el punto está en los lados del cuadro no existe solución, pero tampoco se sabe si hay solución para algún punto fuera del cuadrado.
Por ejemplo: si en el cuadrado de la imagen si el punto p estuviera en A, la distancia a A sería 0 y desde B y D sería 1 (todos racionales), pero desde C sería la raíz cuadrada de 2, que es un número irracional. Si estuviera en el centro del cuadrado, la distancia a cada esquina sería la mitad de raíz de 2 (también irracional) y en puntos del interior se pueden hacer los cálculos con algo tan simple como el teorema de Pitágoras y siempre acaba sucediendo lo mismo.
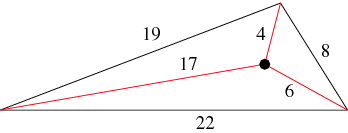
Esta cuestión se conoce como el problema de la distancia racional y curiosamente en otras figuras geométricas como los triángulos sí que existe solución.
Pero el cuadrado de lado unidad es harina de otro costal. Es un ejemplo problema «fácil de explicar, casi imposible de resolver», como el del cuboide perfecto, que es una variante del «ladrillo de Euler» pero también sin solución conocida. También es un problema de esos para los que si existe solución basta con decir: «el punto es el tal, tal». Pero si no la tiene, la demostración es bastante más… complicadilla.
(Vía MathOverflow.)
{Imagen CC0 – creada con GeoGebra}
Relacionado:
- El cuboide perfecto: un problema fácil de entender pero sin solución
- Un problema geométrico de círculos, cuadrados y un área
- Los problemas geométricos de SolveMyMaths
- Un problema de geometría con «sorpresa»
- El problema de los tres triángulos
- Un problema geométrico sobre el envoltorio de un cubo con papel
- Geometría redonda
- El problema del sofá que tenía que pasar por una esquina
- El libro de las matemáticas: una cronología completa e interesante