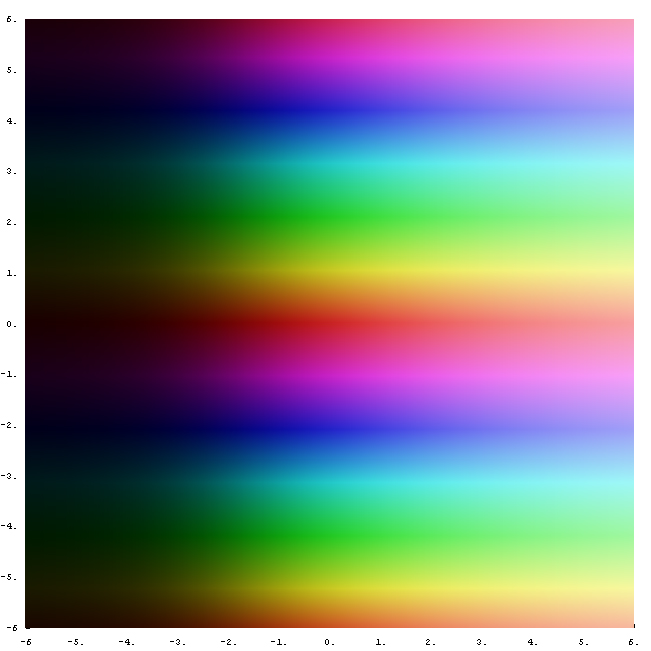
La función exponencial en el plano complejo: el origen de π / Imagen: Jan Homann
A continuación dejo unos enlaces a varios sitios que estuve mirando durante las semanas pasadas, que me parecieron muy interesantes pero que como guardé marcándolos como «Para bloguear…» corren el riesgo de ser procrastinados eternamente. Son estos, sin orden ni concierto pero con muchos hiperenlaces:
#1 – Una fórmula para el enésimo dígito decimal o binario de pi y de potencias de pi
Es un trabajo que alguien publicado acerca de una nueva fórmula para calcular dígitos de pi de una forma novedosa, directa y según parece relativamente sencilla (el paper tiene unas pocas páginas y nada demasiado complicado). Eso sí: los resultados están en binario (aunque eso no es un gran problema) y el algoritmo depende de calcular las secuencias de los números de Euler y Bernoulli, lo cual puede llevar bastante trabajo. Así que como «forma rápida y eficiente» de calcular π con alta precisión queda descartado.
#2 – Verificación de la convergencia en la conjetura de Collatz
En esta página puede verse cómo hay un equipo comprobando con ahínco la conjetura de Collatz, en tiempo real.
Piensa un número cualquiera, que sea entero y mayor que cero. Haz lo siguiente: Si es par, divídelo por dos. Si es impar, multiplícalo por tres y súmale uno. Repite esta misma operación una y otra vez. Al final siempre obtendrás el mismo resultado: 1.
En el momento de escribir esto ya han llegado hasta 677 × 260 (≈ 269,40). Lo más curioso es que puedes recargar la página y ver cómo han avanzado imperceptiblemente más allá.
#3 - ¿Qué es pi? (Y, ya que estamos, qué es e?
Es una interesantísima explicación de Alon Amit en Quora acerca de por qué π es lo que es y de dónde viene. O, dicho de otra forma –y aunque rompa con la forma en la que casi todo el mundo lo aprendió– por qué pi no proviene de las circunferencias y círculos, y por qué aparece en otros lugares de la matemática o la física que no parecen tener nada que ver con los círculos.
En un artículo bastante divulgativo se explica el verdadero origen, que resulta más interesante todavía: la función exponencial (compleja) y en concreto de la más simple: f' = f.


