En las obras de M.C. Escher hay mucha matemática y geometría, pero un poco paradójicamente el propio Escher no se consideraba un gran conocedor de las matemáticas. Reconociendo sus propias limitaciones en más de una ocasión recurrió a la exploración autodidacta, a inspirarse en las matemáticas de otros (como Roger Penrose y sus figuras imposibles) y a consultar a conocidos para analizar lo que surgía de su mente con más detalle e indagar cómo desarrollar nuevas obras.
Ahora en Programming with Escher, de Massimo Santini, pueden leerse algunas notas sobre cómo se pueden utilizar fórmulas matemáticas de transformación y recursión para reconstruir las obras de Escher acerca de teselaciones; lo que solía denominar «la partición del plano mediante patrones».
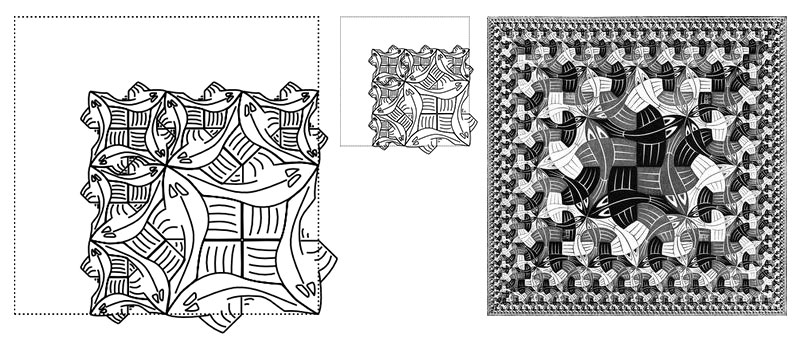
Todo comienza a partir de pequeñas formas cuidadosamente diseñadas (ej. un pez) que se gira, amplía o reduce y colorea. El ejemplo que utiliza es la obra Límite cuadrado (1964) del artista. Pero si el original era una xilografía impresa a partir de tres planchas ahora puede obtenerse más o menos lo mismo con un poco de código en Python 3.
El código está en Github para quien quiera descargarlo, explorar e invesigar. Santini también hace referencia a Functional Geometry, un trabajo de Peter Henderson, donde se explora más formalmente la parte algebraica y matemática del asunto. Al respecto también está muy relacionado Límite circular III, sobre la que se llevó a cabo un análisis similar a partir del Disco de Poincaré y la geometría hiperbólica.
Relacionado,
- Escher y los videojuegos
- Escher en el Palacio de Gaviria
- Mini-biografía de M.C. Escher
- Una divertida casa espiral tan escheriana como extraña
- El universo observable interpretado hiperbólicamente por un artista
- Los patrones de los diseños islámicos
- El triángulo imposible de Lego
- «Relatividad» de M.C. Escher, hecho realidad en el MoMA
- Los reptiles de M.C. Escher en versión parquet para el suelo
- Ascendiendo y descendiendo en nanoblocks
- Las escherianas geometrías de Regolino Bizzi
- Monument Valley: Escher hecho juego
- Estilo Escher
- Una espectacular panorámica del interior del Museo M.C. Escher
- El arte matemático de M.C. Escher
- Límite circular III, de M.C. Escher, en versión animada
- Los universos infinitos de M.C. Escher, en Granada
- Relatividad recortable, arte en papel
- La cascada imposible de M.C. Escher, en el MundoReal™
- Cascada en pixel-art, un clásico pixelizado
- Escher for Real, cómo construir realmente sus obras
- Habitación de Ames en el museo Escher, otro bonito efecto «real»
- Una casa M.C. Escher 3-D bastante realista
- M.C. Escher en LEGO, varias de sus obras, homenajeadas