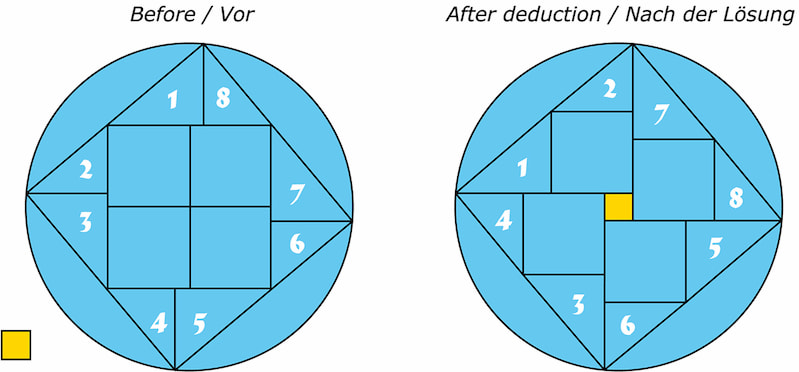
Me encontré este vídeo del canal del Dr. Archimedes sobre un curioso puzle llamado Quadrix o Quinnus, pues tiene varios nombres. Consiste en hacer encajar todas las piezas correctamente, pero la curiosidad es que hay una «pieza extra» amarilla que también se puede colocar aunque sea aparentemente imposible.
La cuestión es que basta reordenar correctamente las piezas del puzle para hacer el hueco justo en el que encaja el pequeño cuadradito. Ahora bien: si el tamaño del cuadrado grande que abarcan todas las piezas aparentemente no varía, y se usan todas las piezas además del cuadradito extra… ¿Cómo demonios sucede esto? Nota: el vídeo no tiene truco y el encaje de las piezas es de una precisión de 0,01 mm.
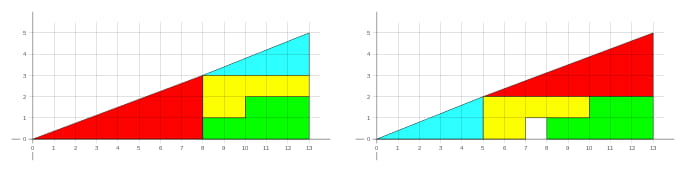
La respuesta es muy interesante y la conocerán quienes hayan visto puzles similares, por ejemplo algunos de los del legendario Sam Lloyd como Get Off the Earth o El duende que se desvanece. Otros que se basan en el mismo principio son la barra de chocolate infinita que se puede «cortar y recomponer» de modo que sobre una onza como por arte de magia o aquella otra paradoja geométrica muy divertida donde no sólo sobra una pieza unidad; sobran dos.
¿Dónde está el cuadradito perdido? (CC) Wikipedia
Recuerdo la satisfacción de haber encontrado la explicación matemática al asunto cuando era quinceañero tras devanarme los sesos con una versión similar, la paradoja del cuadrado perdido descrita en uno de los libros de Martin Gardner. Al parecer esa versión fue inventada por el mago Paul Curry en 1953. Es altamente recomendable analizarlo, es geometría bastante sencilla.
En la página
Quirinus, The Amazing Paradoxical Puzzle, referenciada en el vídeo, se describe el mismo puzle con diversos gráficos y enlaces.
Relacionado:



