Un buen artículo de Manuel Lucena, titulado Protocolos de Conocimiento Cero en Kriptópolis me ha recordado una de las demostraciones más elegantes, sencillas y divulgativas sobre el tema de los Protocolos de Conocimiento Cero (Zero Knowdledge Protocols), algo que en principio parece complicadísimo para el lector medio. De hecho, al comenzar a leer el artículo de Kriptópolis el lector ya se enfrenta a fórmulas y terminología un tanto complicada;
David transforma M para construir un nuevo problema matemático M', cuya solución X' se podrá calcular fácilmente a partir de X, y lo envía a Víctor (...) Víctor genera un bit aleatorio B y lo remite a David (...) Si B=0, David demuestra la relación entre M y M', sin dar la solución a M' (...) Si B=1, David proporciona la solución X' del problema M', sin revelar la relación entre M y M'.
En cambio, existe otra forma de explicarlo bien gráfica y sencilla, mediante lo que informalmente se conoce como prueba interactiva. Creo que la primera vez que lo lei fue en clásico Applied Cryptography de Bruce Schneier. Otro lugar donde leer más sobre el tema es la documentación clásica del FAQ de RSA Security.
En esta prueba interactiva de Conocimiento Cero, una persona trata de demostrar a otra que sabe algo, sin enseñarle o transmitirle ese «algo». En el siguiente ejemplo Alicia quiere demostrar a Bob que sabe las palabras secretas (clave) para abrir una puerta mágica (problema, criptosistema) - sin decir esas palabras delante de Bob (sin enseñarle la clave). La demostración es la siguiente:
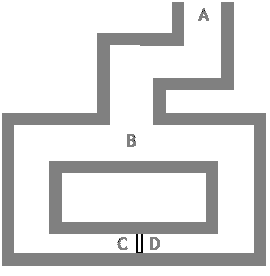
La puerta mágica está en la cueva de Alí-Babá. La cueva tiene una entrada [A] y una bifurcación [B] que llega a ambos lados de la puerta [C y D].
Alicia entra en la cueva, y asegura como demostración que, dado que sabe las palabras mágicas, cuando Bob entre y llegue a la puerta, ella estará en el mismo lugar por el que él entre, dado que puede abrir la puerta y pasar de un lado a otro [C] a [D] antes de que él llegue.
Alicia entra desde por cualquier camino. Cuando Bob comienza a entrar y llega al punto [B], decide si continuar por la izquierda o por la derecha. Puede gritarle a Alicia por donde va a ir, o sencillamente Alicia oye los pasos de Bob: si escucha que entra por el mismo lado en el que ella está, le espera allí. Pero si entra por el lado contrario, usa las palabras máginas para abrir la puerta y volverla a cerrar, apareciendo en el lado correcto. Bob llega a la puerta [C] o [D] y encuentra a Alicia, y también comprueba que la puerta está cerrada.
Si este protocolo («demostración») se realizara sólo una vez, Bob podría pensar que Alicia ha tenido suerte al entrar en la cueva, esperándole en el lado correcto (la probabilidad es del 50 por ciento). De modo que se repite la operación. Alicia vuelve a acertar. Una vez más... y Alicia vuelve a estar allí. Bob puede repetir el protocolo cuantas veces quiera, y tras un número de veces razonable (diez o veinte) le empieza parecer imposible que Alicia haya tenido tanta suerte como para acertar siempre. Si Bob repitiera el protocolo mil veces, la probabilidad de que Alicia acertara por puro azar sería infinitesimal. De modo que es cierto que Alicia sabe algo, aunque no le haya transmitido ese conocimiento a Bob .
Actualización (18 de abril de 2020) – Por desgracia el artículo original parece que ya no existe.


