Ya hemos comentando aquí que los seres humanos no somos muy buenos en ciertas técnicas matemáticas (calcular probabilidades, entender los grandes números o el crecimiento exponencial). Pues bien: tampoco somos muy buenos generando secuencias de números al azar. Dos minutos bastan para entender porqué.
La forma de comprobarlo es imaginar dos habitaciones cerradas: en una de ellas alguien lanza una moneda al aire y señala un 1 o un 0 según salga cara o cruz. En la otra, una persona intenta hacer lo mismo pero sin usar ninguna moneda, simplemente «con la cabeza». Ambas secuencias son intencionalmente aleatorias… ¿Se puede distinguir la «auténtica» (moneda) de la «imitada» (persona)?
La forma de comprobar la aleatoriedad de las secuencias pasaría simplemente por contar el total de ceros y unos tras disponer de cientos de resultados: más o menos habrá la mitad de ceros y la mitad de unos. ¿Y luego? Basta comprobar la estabilidad de las frecuencias en secuencias más largas: por ejemplo se podrían comparar las secuencias 00 01 10 y 11 (que deberían aparecer un 25 por ciento de las veces cada una), luego 000 001 010 011 100 101 110 111 (un 12,5% cada una), luego 0000 0001 0010, etcétera.
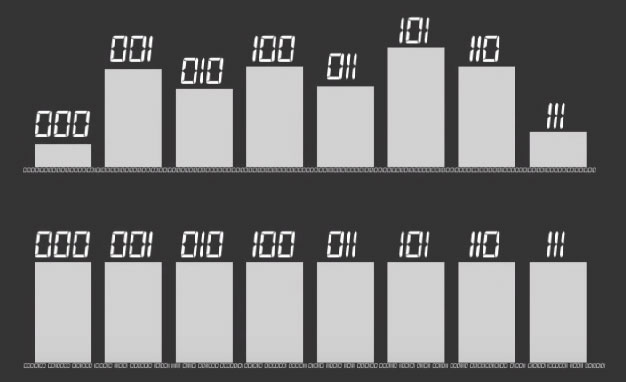
La imagen (un tanto dramatizada) no deja lugar a dudas. ¿Cuál es genuinamente aleatoria? ¿Cuál tiene algún tipo de sesgos? ¿En cuál una persona habría intentado «engañar» para que pareciera aleatoria? Claramente en el primer caso: el segundo histograma muestra que todas las secuencias tienen la misma probabilidad –más o menos– de aparecer a la larga, que es precisamente, una de las leyes del azar y la aleatoriedad.



