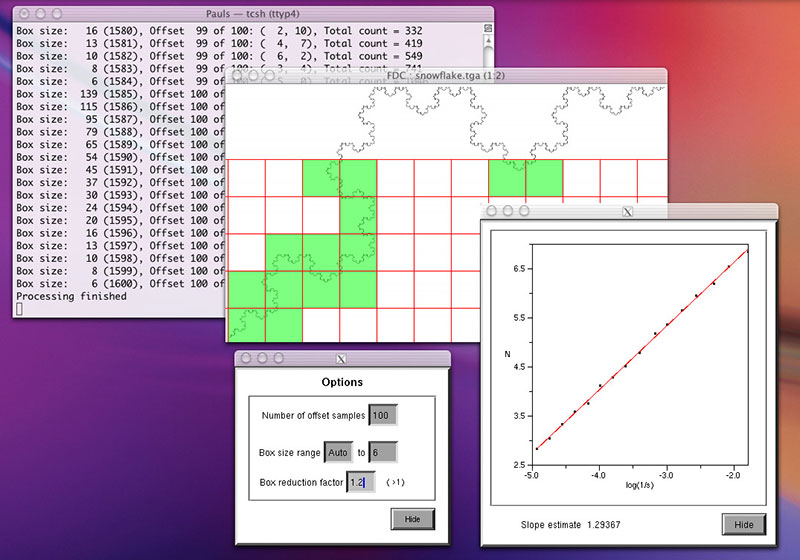
La Calculadora de Dimensión Fractal (FDC) de Paul Bourke calcula cuál es la dimensión fractal de una curva según el relleno de píxeles que tenga. Es un método sin duda tosco pero bastante aproximado. Los cálculos exactos son algo más complicados.
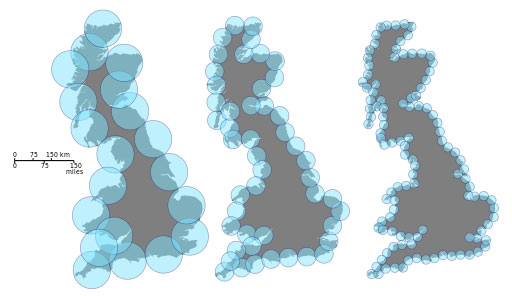
Esto de la dimensión fractal tiene que ver con aquello de ¿Qué longitud tiene la costa de Inglaterra? Matemáticamente «depende de cómo se mida». Topográficamente tiene 12.429 kilómetros, pero esa no es la cuestión. Si se usa una «regla» de distintas longitudes puede ser tan corta o larga como queramos. Es un «parece que es» «pero no» «pero a veces», una de las rarezas del apasionante mundo fractal:
La dimensión fractal es un exponente que da cuenta de cuán completamente parece llenar un fractal el espacio conforme se amplía el primero hacia escalas más y más finas. No existe una única dimensión fractal sino una serie de dimensiones que, frecuentemente, resultan equivalentes aunque no siempre.
Tomemos por ejemplo la famosa Curva o Copo de nieve de Koch. Se crea entresacando puntas a los lados de lo que originalmente es un triángulo. En ese triángulo si el lado original mide 1 su perímetro sería 3. Tras la primera iteración pasa a haber 4 lados iguales, de modo que la longitud serían 4/3 del original en cada lado, es decir 3 × 4/3.
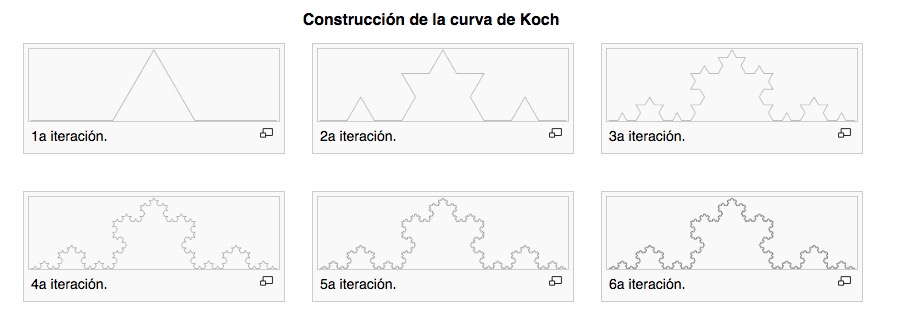
Al repetir este proceso una y otra vez –y teniendo en cuenta que por su construcción la curva nunca se corta a sí misma– la longitud al cabo de n pasos sería 3 ×(4/3)n, que tiende a infinito a medida que aumenta n. Si embargo la superficie del copo no es infinita, pues está siempre confinada a poco más allá del triángulo original. ¿Qué clase de brujería es esta? ¿Puede una curva de longitud infinita delimitar una figura finita? Nada lo impide: esa es la curiosa propiedad de este y otros fractales.
La dimensión del Copo de nieve de Koch está por tanto entre 1 (una línea) y 2 (una figura plana); de hecho puede calcularse exactamente y resulta ser de ~1,2618. Es lo que se llama dimensión de Hausdorff-Besicovitch. En el caso de la esponja de Menger que es «casi tridimensional, pero no» su dimensión es ~2,7268.
En otros objetos topológicos los cálculos pueden ser bastante más complicados, por eso la Calculadora de Dimensión Fractal viene bien para obtener al menos una aproximación rápida.


