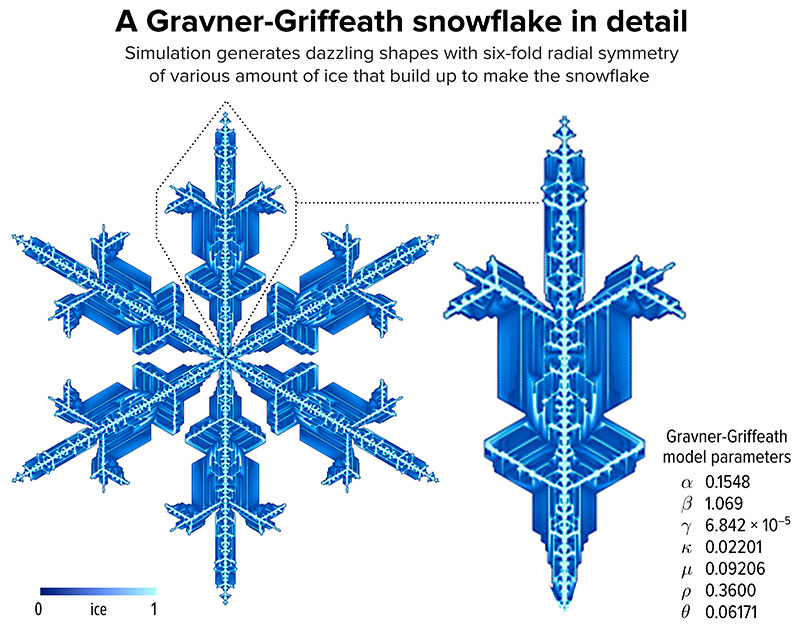
Krzywinski y Lever publicaron un precioso y bastante complejo artículo en Scientific American acerca de la creación de copos de nieve mediante modelos matemáticos. In Silico Flurries describe cómo utilizar un modelo que hace crecer estos intrincadas maravillas de la naturaleza a partir de una rejilla hexagonal y siete parámetros distintos, que tienen que ver con sus tres estados (líquido, cuasi-líquido y vapor de agua) y diversos factores acerca de cómo se condensan y derriten sus moléculas.
La característica forma hexagonal de los copos (aunque en ocasiones pueden existir con formas como triángulos o rombos) tiene que ver con cómo se acomodan las moléculas de vapor de agua (oxígeno + hidrógeno), las pequeñísimas impurezas –como las motas de polvo– y a fenómenos como la supersaturación y el superenfriamiento.
Debido a que cualquier mínimo cambio de temperatura supone una gran variación en la forma resultante, esto afecta al «crecimiento» de los copos. Incluso la forma de la propia estructura afecta a esas temperaturas localmente, lo que se ve reforzado cuando el copo se está moviendo libremente por el aire. Por eso se dice que «no existen dos copos de nieve iguales». Esto es básicamente cierto, aunque con suficiente esfuerzo se pueden hacer crecer copos de nieve gemelos en un laboratorio bajo condiciones estrictamente controladas.
La exploración matemática de los autores para crear unos copos bastante «creíbles» es realmente enrevesada – y va incluso más allá de los copos de nieve, así que lo mejor es ver los ejemplos y disfrutar de su belleza. Quien lo desee puede investigar el trabajo original basado en el llamado modelo Gravner-Griffeath o explorar las líneas de código de estos modelos.
Bonus: nunca está de más volver a recomendar el precioso libro What Shape is a Snowflake? Magic Numbers in Nature, de Ian Stewart, dedicado precisamente a los copos de nieve (fractales y un poco caóticos) como tema central, aunque cubre infinidad de otros temas interesantes.
Relacionado:
- Los copos de nieve vistos de otra forma
- Copos de nieve en fotografías
- ¿Por qué existen algunos copos de nieve triangulares?
- Así se forma un copo de nieve – vídeo
- La belleza de un copo de nieve, a 36.000 aumentos
- La ciencia echa por tierra la creencia de que no hay dos copos de nieve que sean iguales