Este artículo se publicó originalmente en Cooking Ideas, un blog de Vodafone donde colaboramos semanalmente con el objetivo de crear historias que «alimenten la mente de ideas».
A muchos seres humanos no les gana a cabezones nadie. Una buena muestra de ello son aquellos que persiguen lo imposible, entendido como tal lo que es matemática o físicamente imposible. Y es que tal vez la fama o la búsqueda de los hallazgos épicos –por no hablar del simple y llano desconocimiento de la ciencia– son una gran motivación para gente con mucho tiempo libre.
Aquí van un par de esas tareas imposibles que la gente se empeña en perseguir inútilmente, en algunos casos desde hace milenios:
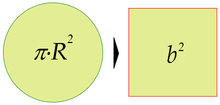
1. La cuadratura del círculo: ¿Se puede, utilizando sólo regla y compás, dibujar un cuadrado que tenga la misma superficie que un círculo dado? Con una regla infinitamente precisa la cuestión sería casi trivial pero… ¿Sólo con regla y compás? Los griegos, que de geometría sabían mucho, persiguieron esta cuestión imaginando que habría algún enrevesado para resolverlo, pero sin hallarlo – y eso a pesar de que problemas similares o aparentemente más complejos sí que tenían solución. Como nadie conseguían dar tampoco con una demostración de que la operación fuera imposible, durante siglos un montón de matemáticos se entregaron en cuerpo y alma a la cuestión.
En el fondo el problema tiene que ver con la naturaleza del número pi: dada la infinitud de sus decimales (matemáticamente, se denomina un número trascendental) es imposible afinar tanto como para construir algo igual de preciso, en este caso un cuadrado equivalente en superficie. En la práctica basta utilizar una aproximación razonable para pi (como 22/7 o 355/113) para dar con un resultado humanamente adecuado. Pero, científicamente, hubo que esperar a finales del siglo XIX a que el matemático Ferdinand Lindemann demostrara la transcendencia de pi para zanjar la cuestión: pi era un número transcendente y la construcción exacta según el enunciado del problema era imposible.
¿Y qué sucedió después? A pesar de que haber demostrado que el problema era tan imposible como que al sumar 2+2 el resultado fuera 5, muchas almas ingenuas siguieron durante todo el siglo XX buscando una solución. Algunas no sabían que ya se había demostrado que era imposible; otras hicieron oídos sordos y siguieron encabezonadas. De hecho todavía hoy en día muchos profesores reciben «demostraciones» sin mucho rigor de gente sin grandes conocimientos pretendiendo haber resuelto el problema. ¿Qué hacer con todo ese papel? La tradición dice que lo mejor es entregar las «demostraciones» a los estudiantes de primer curso para que encuentren «dónde está el fallo», respondan a los autores y se apunten unos puntos extra.
2. El movimiento perpetuo. ¿Has visto alguna vez una de esas máquinas que se mueven sin parar, con bolitas, imanes, agua, movimientos pendulares, giratorios o giroscópicos, que parecen no pararse nunca? Todas ellas son simples juguetes o simulacros de móviles perpetuos, una categoría en la que se encuadran aparatos de todo tipo que parecen moverse sin fin y sin energía que los impulse, salvo quizá para la puesta en marcha.
La clave del asunto es precisamente que un aparato de este tipo no necesitaría energía externa que lo impulsara; sería un sistema cerrado, independiente y «eterno». Pero lo cierto es que de un modo u otro incluso los más complejos utilizan de algún modo energía externa (viento, luz solar, electricidad…) y no son verdaderos móviles perpetuos: algún día no habrá viento, se consumirá el sol o se acabarán las baterías.
El resumen visto de otro modo es que esos ingenios violan la segunda ley de la termodinámica que –en términos llanos– viene a decir que siempre hay una parte de la energía no aprovechable que se pierde debido al rozamiento, el calentamiento y cuestiones similares. Si la primera ley dice que la energía no se crea ni se destruye sino que solo se transforma, la segunda viene a añadir que además se transforma «con pérdidas». Aunque en una explicación estricta habría que hablar de la entropía y otros conceptos un tanto abstractos, basta con quedarse con esa idea de que «si ya tienes una cantidad de energía, no puedes retorcerla ni manipularla si ayuda exterior para tener más».
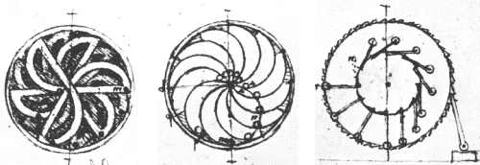
Aunque esta ley se conoce desde antiguo y fue descrita formalmente también en el siglo XIX por varios físicos, desde tiempos ancestrales muchos ingenieros e inventores muy, muy cabezotas, han intentado crear mecanismos perpetuos: giratorios, con poleas, corrientes de agua, imanes, bolitas, molinillos de aire y todo tipo de detalles ingeniosos. La eterna búsqueda del perpetuum mobile. Leonardo y otros clásicos le dedicaron algo de tiempo en vano. Para ninguno dio resultado: todos fallan porque no se pueden poner en marcha, se paran al poco tiempo o es imposible eliminar de ellos el rozamiento para mantenerlos funcionando. Los más modernos utilizan electricidad en diversas formas: electroimanes, giroscopios, superconductores y elementos más raros todavía.
Naturalmente, todos esos móviles perpetuos ni funcionan ni funcionarán: si alguno lo hiciera, no solo violaría la segunda ley de la termodinámica, también produciría energía extra que sería fácil acumular o vender y haría infinitamente rico a su inventor (tal vez por eso haya tanto pirado de los móviles perpetuos suelto). Internet está lleno de bromas y sistemas perpetuos graciosos, así como de otros más complejos que son auténticos timos para sacar dinero a la gente corriente o a inversores con ganas de tirar su dinero. Así que, como entretenimiento están bien, pero cuando alguien menciones un «móvil perpetuo» como negocio… ¡Cuidado!
{Fotos: Perpetuum Mobile (CC) Rene Schwietzke @ Flickr; Cuadratura del Círculo (CC) Haylli @ Wikipedia; Perpetuum Mobile de Leonardo da Vinci.}