La Paradoja de Bertrand o Paradoja de la Cuerda Aleatoria es un interesante problema de probabilidad y geometría. Tiene la peculiaridad de ser una paradoja debido a que existen varias soluciones contradictorias. Debe su nombre a Joseph Bertrand, quien la publicó en 1888.
El problema suele enunciarse así:
Supongamos que se elige al azar una cuerda de un círculo. [Una cuerda es una línea que une dos puntos de su circunferencia.] ¿Cuál es la probabilidad de que la longitud de esa cuerda sea mayor que la del lado de un triángulo equilátero inscrito en dicho círculo?
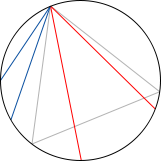
En la imagen de abajo procedente de Wikipedia se ve en gris el triángulo y en azul y rojo distintas cuerdas aleatorias. Las cuerdas azules son menores que el lado del triángulo, las cuerdas rojas, mayores.
Las tres posibles formas de encontrar una solución parecen todas igual de lógicas: el asunto depende de cómo se elijan los «puntos al azar» para formar la cuerda y cómo se razone a partir de ahí, en base a los arcos, radios y otro tipo de construcciones intermedias para razonar la posible solución. Por ejemplo: ¿Se eligen dos puntos de la circunferencia que definan la cuerda? ¿Se elige un radio al azar y se traza una cuerda perpendicular a un punto de ella al azar? ¿Se elige un punto cualquiera del círculo y se toma como punto medio de la cuerda?
Lo curioso es que según se haga de una forma u otra se obtiene que la probabilidad puede ser 1/2, 1/3 ó 1/4. Todas son correctas y de ahí proviene la paradoja.
Cuando se estudia el problema en profundidad es cuando se llega a la conclusión de que la paradoja proviene del término «elegir al azar» del enunciado, de qué se entienda exactamente por ello. Si en vez de dejarlo en el aire se define cómo se eligen al azar los puntos de la cuerda, el problema tiene una solución bien definida. Si no se hace, se puede llegar a varias, todas perfectamente válidas.
Del mismo modo, aunque todas las soluciones son válidas, se consideran unas más satisfactorias que otras, dependiendo de si se interpreta el problema como algo puramente matemático o con una equivalencia física, algo más curioso todavía.
Se pueden ver detalles sobre todo esto en
- Bertrand's paradox (probability) en la Wikipedia, donde están muy bien explicados los tres razonamientos que producen resultados distintos.
- Bertrand’s Problem en MathWorld, con un planteamiento ligeramente distinto pero equivalente.
- Random Chord Paradox, que incluye simulador [Java] que muestra gráficamente los resultados de los tres métodos.
Actualización (22 de diciembre de 2021) – Un buen vídeo de Numberphile donde Grant Sanderson, creador de 3blue1brown, explica la paradoja en cuatro versiones diferentes.