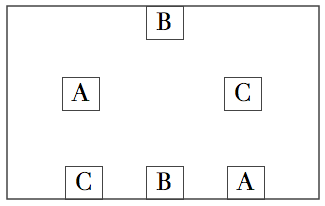
En el problema planteado ayer había que conectar las cajas con las mismas letras con líneas que no se cruzaran. La pregunta principal era:
¿Es posible resolver el problema?
Demuéstralo
En general tendemos a buscar con ahínco la solución de un problema mientras pensamos que existe una solución. Si no estamos seguros, podríamos pensar que es absurdo dedicarle tiempo a algo que es imposible de resolver, en cuyo caso suele ser más fácil plantearse si hay forma de demostrar que existe una solución o de lo contrario.
En el caso del problema de las cajas, si como pista nos dicen que no existe una solución lo complicado suele ser la demostración, que puede ser más o menos rebuscada o rigurosa.
En cambio si damos por hecho que tiene solución, resolver el problema es casi trivial. Si ayer no pudiste resolverlo, y teniendo en cuenta que no hay truquis raros en el planteamiento (como usar 3-D, atravesar las cajas, superponer líneas, etcétera) y que se pueden usar líneas rectas o curvas tan enrevesadas como se desee, inténtalo de nuevo: Sí, se puede resolver. Comienza por unir A-A.
Aquí abajo está la pista definitiva, uniendo C-C, que es el segundo paso, y que está a solo un paso de la solución.
.
.
.
.
.
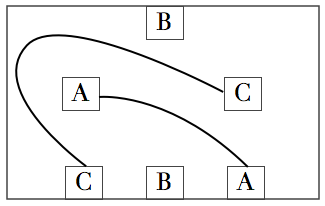
Tan solo falta un tramo en forma de «2» que una B-B y problema resuelto.
¿Era fácil, no? Pues en realidad sí y no: es fácil si se sabe que existe una solución, pero mucha gente puede dar el problema por imposible simplemente por no poder anticipar si se puede resolver o no, que era la cuestión original. En resumen, la respuesta es Sí y la demostración consiste simplemente en mostrar el dibujo; en cambio conseguir una demostración de lo contrario («No es posible») es... imposible, y puede atorar la cabeza a más de uno.


