Encontré este increíble problema-rompecabezas en The Millennium Problems de de Keith Devlin, donde se cita que proviene de Mathematics: The New Golden Age, del mismo autor. (Las imágenes son de Andreas Joensen, las mismas del libro). Se trata de un problema topológico, como Los puentes de Königsberg (todo un clásico), aunque este Problema de los Anillos no sé si es más reciente o está en la lista de los típicos problemas de primer curso de topología (yo no lo conocía y mira que me gustan).
En topología las formas son continuas y deformables, se suele decir que es como «la geometría de las figuras de goma». Propiedades como longitud, orientación o posición son irrelevantes, mientras que otras como «número de agujeros» son más importantes. Se suele decir que un topólogo «no distingue un donut de una taza de café», porque ambas formas son «topológicamente equivalentes»: si estuvieran hechas de material flexible, se podría deformar una de ellas hasta llegar a la otra, y viceversa (ambas tienen un «agujero»).
Hay cuestiones topológicas en dos, tres y más dimensiones. Muchos son fáciles de entender, como el problema de los cuatro colores. Aunque eso no quiere decir que sean fáciles de resolver. Los mejores matemáticos necesitaron siglos para resolver ese problema.
Este Problema de los Anillos está entre los que cualquiera puede resolver con una combiación de vista, paciencia y razonamiento Se trata de una figura trimensional, una especie de «llavero de goma» con dos anillos (A):
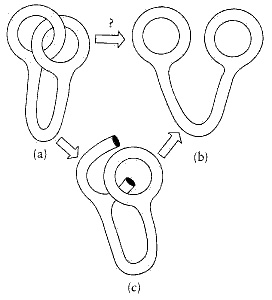
¿Se puede tranformar la figura de anillos (A) en (B)?
Las «reglas topológicas» exigen no «cortar» la figura por ningún punto. Una forma obvia de llegar de A a B sería como se ve arriba cortar uno de los anillos como en C, separarlos y luego volver a pegarlos. Sin embargo esto no es admisible dentro de las reglas. Sólo se puede deformar, mover y retorcer la figura cuanto se quiera (su elasticidad es infinita) pero no se puede cortar ni agujerear.
Este es el momento en el que hay que mirar y remirar (A) y (B) y razonar hasta decidir si hay alguna forma de transformar (A) en (B) o si, por el contrario, se puede demostrar que es imposible esa transformación.
La solución, a continuación:
.
.
.
.
.
.
.
.
Aunque parezca increíble y sorprendente, la solución al problema es que sí se puede transformar (A) en (B) sin cortar en ningún momento el objeto. Basta con deformarlo de la forma adecuada.
Ahora que sabes que es posible hacerlo tal vez quieras volver a mirar el objeto, a ver si descubres cómo se puede pasar de (A) a (B).
La solución, un poco más abajo.
.
.
.
.
.
.
.
.
La transformación que hay que realizar es esta:
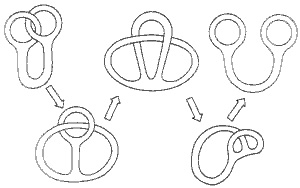
Partiendo de (1) en primer lugar el lado derecho se alarga y deforma (2) mientras los anillos siguen uno dentro del otro. Después el «cuello» del primer anillo desciende (3) abriéndose por la base. A continuación (4) se saca ese anillo vertical del otro, por uno de los lateriales (este paso es el más difícil de ver, pero imaginando la figura (3) de forma tridimensional «desde lejos» es fácil ver que el anillo vertical puede «salir», aunque no se parezca mucho al dibujo 4). La forma final (4) mantiene los dos agujeros; un poco de transformación (5) y... ¡Listo! Los dos anillos quedan separados.
Esta increíble solución me hizo pensar en un problema equivalente que siempre me intrigó: si unes tus manos como dos anillos cruzados, una contra otra (formando un anillo con los pulgares y el índice «pegados» en cada mano) eres un objeto equivalente a la figura A, mientras que con las manos separadas eres como la B. Esta solución quiere decir que, si fueras muy elástico, podrías desenredar esa forma aparentemente imposible porque topológicamente eres el mismo objeto. Y todo eso... sin aprovechar la topología propia de los orificios corporales naturales ;-)


