Esta maravilla se llama Pattern Collider y es una genialidad de aplicación creada por Aatish Bhatia y Henry Reich para explorar patrones de teselaciones cuasiperiódicas. Es de esas cosas más complicadas de explicar que de probar, así que lo más fácil es empezar a mover el ratón y los controles para disfrutar de las formas que, casi mágicamente, encajan unas con otras a la perfección.
Esta teselaciones son una forma geométrica muy curiosa de dividir el plano, donde las formas que se utilizan no se repiten aunque el mosaico se gire o desplace en cualquier dirección. Esto es distinto de las teselaciones habituales con triángulos, cuadrados, hexágonos o combinaciones similares de polígonos regulares. Una de las más famosas es la teselación de Penrose, pero hay muchas otras y esta herramienta permite explorarlas. (Hay una muy buena explicación de todo esto en un vídeo, precisamente utilizando Pattern Collider, en Minute Physics).
Hay tres pestañas con controles: Patrones, Tamaño y Color. Las dos últimas son puramente decorativas y en la de los patrones se pueden modificar:
- Orden de la simetría (de 3 a 19)
- Patrón
- Rotación
- Desplazamiento
- Desorden
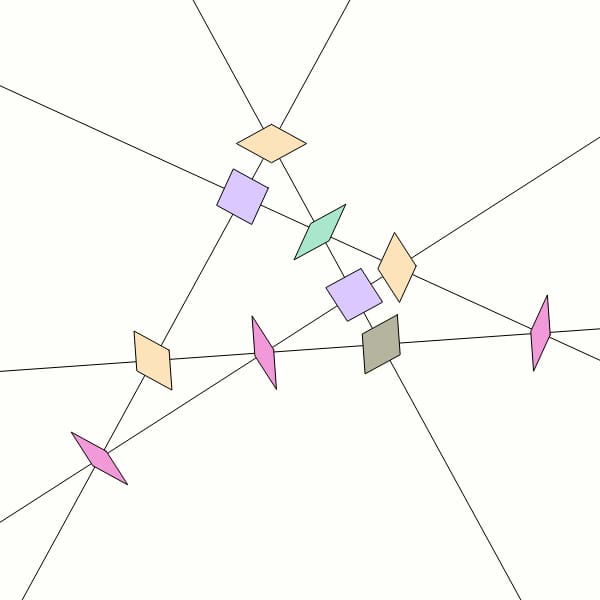
También hay botones para randomizar (generar un patrón aleatorio) y las opciones de coloreo y tamaño permiten afinar los tonos de color, contraste, zoom, etcétera. La pantalla se divide en dos: una multirejilla (grid) que fue un descubrimiento de Nicolaas Govert de Bruijn y que permite crear estas simetrías trazando algunas rectas y asignado polígonos equiláteros a las intersecciones. Una vez creada la forma básica se puede incluso colorear pieza a pieza, si tienes paciencia para ello.
Los resultados se pueden guardar en formato .svg para la posteridad (tanto la rejilla como el patrón ya generado), o compartir mediante enlaces. Además del puro entretenimiento de «explorar por explorar» es una herramienta que puede ser útil para algunas labores de diseño o incluso para la creación de isotipos de esos que están tan de moda. Además de todo esto, el código fuente está disponible en Github.
Relacionado:
- De la simetría a la metaquiralidad
- La Teselaciones de M.C. Escher en GeoGebra
- Un Bach más geométrico todavía
- Poliedros para todos los gustos
- La geometría islámica vista por Samira Mian: diseños y vídeos
- El arte matemático de M.C. Escher
- Polygonia: diseño de teselaciones y patrones
- Las rejillas hexagonales explicadas con geometría y algoritmos
