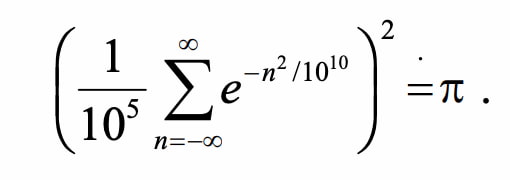Me sorprendió un tanto cruzarme con esta referencia a una fórmula de π en la que se da una fórmula bastante breve y aparentemente sencilla al menos de aspecto para el número pi. Ahora bien, se trata de es una fórmula «incorrecta», cuyo resultado es muy parecido a π, pero no es exacta. El cómo se deducen y comprueban este tipo de detalles es toda una aventura matemática.
La fórmula al parecer procede de un trabajo de Thomas J. Olser, un profesor de matemáticas e informática que la publicó en 1998 en un trabajo titulado, apropiadamente, Get Billions and Billions of Correct Digits of Pi From a Wrong Formula (Cómo obtener miles de millones de dígitos correctos de pi a partir de una fórmula errónea). Se puede descargar el PDF completo, que son tan solo ocho páginas.
Tal y como cuenta Olsen, la fórmula genera unos 42.000 millones de decimales correctos, pero al llegar a los 43.000 millones el resultado ya difiere de pi, por lo que puede considerarse a tales efectos incorrecta. La explicación matemática al respecto parece que tienen que ver con una función theta, la raíz cuadrada de pi, y otras cuestiones matemáticas que a mi se me escapan, pero ahí están para quien quiera curiosear. Según he entendido tiene que ver con que el 1010 de la fórmula tiene unos 42.000 millones de dígitos y hacia el final del desarrollo del cálculo de la raíz cuadrada de pi (por eso la fórmula va elevada al cuadrado para «compararla» con pi) hay una resta de dos expresiones. Al no ser exactamente cero quiere decir que las expresiones son diferentes y a partir de esos decimales surge algún otro valor.
El trabajo original decía que, curiosamente, a fecha de su publicación (1998) tan sólo se habían calculado unos 51.000 millones de decimales de pi, por lo que si se calculara el resultado de la fórmula se observaría esa divergencia en cierto punto a partir de los 42.000 millones de decimales. En la práctica nadie lo ha hecho porque aunque se conocen fórmulas bastante eficientes para calcular decimales de pi (el récord actual va por 50 billones de decimales, 1.000 veces más que el de 1998) el cálculo de la fórmula de Olsen es muy ineficiente y tedioso, por lo cual no tendría seguramente mucho sentido.
(Vía el siempre acertado @Pickover.)
Relacionado:
- Cómo calcular el valor de π por diferentes métodos
- Una recopilación de algoritmos para calcular el valor del número π
- ¿Para qué sirve conocer o calcular millones y millones de dígitos de π?
- Cómo calcular el valor de π por diferentes métodos
- El ingenioso método de Arquímedes para calcular el valor de π
- Mechanical pi, o cómo calcular π de una forma especial
- Cómo generar los decimales de π con programas cortos e ingeniosos
- El valor de pi como «solución inesperada» a un problema matemático
- Usos prácticos de los decimales de pi
- Una simulación de Montecarlo para calcular el valor de π
- El número π en el papiro matemático Rhind de hace 4.000 años
- La evolución de Pi con el tiempo