Esto es para los más frikis de los números, la estadística y el azar. Resulta que publicaron un trabajo titulado Sloane’s Gap: Do Mathematical and Social Factors Explain the Distribution of Numbers in the OEIS? [PDF] del que nos habla la gente de Numberphile. Básicamente tiene que ver con el extraño comportamiento de los números naturales en un contexto en el que la intuición nos dice que deberían comportarse de otro modo – de ahí la aparente extrañeza que genera el tema.
El asunto tiene su miga: está relacionado con la popular web Enciclopedia Online de Secuencias de enteros (OEIS) en la que Neil J. A. Sloane lleva años recopilando secuencias de números enteros importantes: desde la lista de los números pares a los números primos, los números perfectos, etcétera… (por aquí ya hemos hablado de ella alguna vez). La enciclopedia es tan vasta que se pueden teclear varios números y ver a qué corresponden: quizá sean las formas de conectar un grafo planar de n puntos, los números chungos de Lost o las posibles formas de plegar un mapa.
El caso es que esa base de datos contiene miles de entradas, y alguien se entretuvo en recopilar todos los números en ella aparecen y plotear un gráfico. Como era de esperar, algunos números son más «populares» que otros, quizá porque son más bajos, más «redondos» o tienen alguna propiedad que forma parte de muchas secuencias (ser un número primo, o cuadrado, o perfecto…)
El gráfico es este: en horizontal estarían los números naturales que aparecen en alguna secuencia y en vertical [log] las veces que aparece en la enciclopedia:
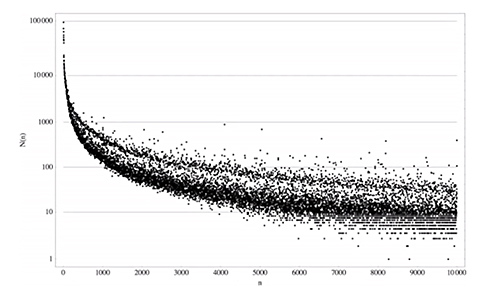
Números como el 0, 1, 2… aparecen más de 100.000 veces, mientras que a partir del 100 aparecen ya solo 10.000, hasta el 1.000 aparecen uno poco menos de mil veces (excepto el propio 1.000) y a partir de ahí la gráfica continua en una grácil curva. Los puntitos sueltos que destacan hacia arriba corresponden con los números más redondos: 4.000, 5.000, 8.000, 10.000… Ni idea de cuál es el famoso número que está entre el 6000 y el 7000 que es más «popular» en las secuencias que el 9.000, pero ahí está.
Ahora bien… ¿qué demonios es esa banda sin apenas valores que aparece en el centro de la curva? En general parece que los números más redondos, primos, cuadrados y similares con alguna propiedad curiosa están por encima; el resto, los del montón, debajo. Pero tampoco parece ser un efecto como el que sucede en la Ley de Benford, que hace que todos los números suelan empezar por «1».
Los matemáticos franceses que estudiaron el asunto y escribieron el trabajo al respecto creen que eso indica la complejidad del número en términos de «cómo se define» dicho número entero: cuanto más simple es de describir, más popular es. También añadieron que puede haber un factor «social» que hace que la comunidad matemática interesada en los números enteros y las secuencias haya subido a la base de datos muchos números «complejidad intermedia» (porque son más interesantes, como los de tipo 2n+1, útil al estudiar números primos) lo cual distorsiona también un poco el gráfico.
Su conclusión es tan intrigante como el propio gráfico: no hay un solo factor matemático que explique por sí solo el hueco que deja la franja de Sloane, especialmente si no se tienen en cuenta las consideraciones «sociales».


