Para presentar la archiconocida paradoja del cumpleaños se suele hacer ver a la gente reunida en una clase cuántas personas hay –quizá 30 ó 40– y que un año tiene 365 días. Luego se pregunta si creen probable que dos personas cumplan años el mismo día; también se puede pedir estimar cuántas personas harían falta para que la probabilidad de que esto suceda sea más del 50%. Con un número de gente grande –pero tampoco hace falta que sea inmenso– hay quien incluso propone apostar dinero de verdad, sabiendo que tiene las leyes de la probabilidad a su favor, como demuestran algunos cálculos.
Y es que este efecto se denomina paradoja porque el resultado es contrario a la intuición: hacen falta tan solo 23 personas en un grupo para que esta probabilidad sea más del 50%. La clave es que el problema pide «que dos personas cumplan años el mismo día», no que haya alguien que cumpla el mismo día que otra persona en concreto. En primer caso, 23 personas pueden formar 253 parejas distintas, y todas son candidatas. Si nos refiriéramos sólo a una de las personas en concreto sería de 1/365 para cada una de las 22 personas, (22/365) = ~6% en total, que es mucho menos. (Nota: Se suelen ignorar los años bisiestos.)
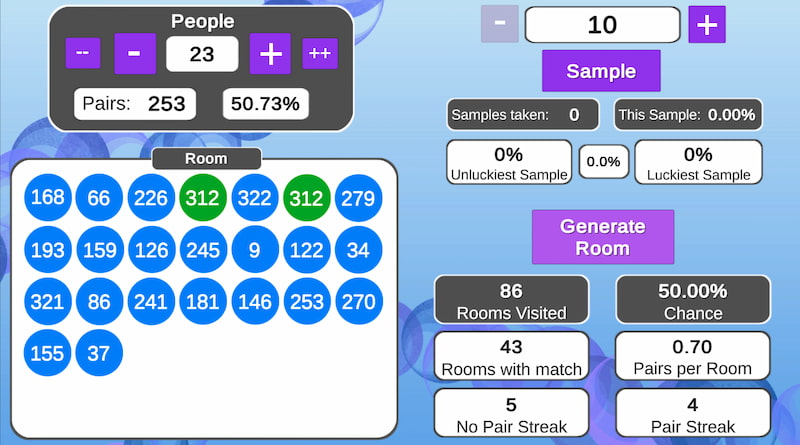
Para que se vea más claro Brain Feast ha convertido todo esto en un Simulador de la Paradoja del Cumpleaños en Unity, donde hay botones para pulsar y modificar ciertas variables:
Se puede aumentar o disminuir el número de personas (People) en cada habitación, y pulsando en Generar habitación (Generate Room) se eligen las fechas para todas las personas, con número entre el 1 y 365 que simboliza todos los días del año.
Como resultados, los colores indican si las fechas no se repiten (rojo) o coinciden (verde); de hecho a veces coincide más de una pareja. Lo más interesante es que se pueden generar muestras aleatorias de 10 en 10, o de 100 en 100 o en múltiplos de 10 (botón Sample) para hacer pruebas más rápido. Los paneles de la parte inferior derecha acumulan y promedian los resultados para que se vea cómo de significativa es la estadística a medida que evoluciona (en el simulador esto se explica como «número de habitaciones visitadas»).
Aumentando el número de personas en la habitación es fácil ver cómo cada vez es más difícil evitar que coincidan dos fechas; en el caso límite en una habitación con 365 personas sería prácticamente imposible que no hubiera coincidencias, porque cada persona tendría que haber nacido exactamente en un día distinto del año.
Además de comprobar cómo el famoso valor de 23 es numéricamente preciso en el caso de las fechas de cumpleaños para superar esa barrera del 50% (concretamente la probabilidad es 50,7%; en el caso de sólo 22 personas es sólo del 47,6%) lo más importante de esa paradoja es saber reconocerla en otras situaciones. Una vez asimilada, muchas de esas «coincidencias increíbles» que observamos en nuestra vida cotidiana dejan de ser tales, porque el número de «posibles coincidencias» es tan grande que a veces resultan ser sucesos más probables que improbables.
Relacionado: