Me crucé con vídeo de una calculadora ternaria que muestra cómo operaba la máquina calculadora ternaria de Thomas Fowler, un artilugio construido en 1840 que basaba su funcionamiento en la base 3 (en vez de 2 del binario o el 10 del decimal). Y es que hasta que los ingenieros, inventores e informáticos se pusieron de acuerdo en que el binario era lo más adecuado para trabajar con las computadoras electrónicas se probaron muchas otras ideas básicas.
Las cosas en la calculadora ternaria de Fowler eran un poquito más complicadas todavía: en vez de utilizar como valores 0, 1 y 2 de lo que sería el sistema de numeración ternario empleaba la llamada aritmética ternaria equilibrada con el equivalente de -1, 0 y +1 para los cálculos. «En el fondo es lo mismo», podría decirse, pero lo cierto es que esa idea simplificaba algunos cálculos y operaciones (como restar e incluso multiplicar) y además lleva implícita el concepto de los números negativos – cosa que en binario requiere reservar un bit para el signo.
Todo esto y mucho más lo cuenta Marianne Belloti en The Land Before Binary (La tierra antes del binario), un estupendo y completo artículo donde cuenta más sobre estos «sistemas alternativos de numeración para computación». Los soviéticos, por ejemplo, también probaron con máquinas ternarias.
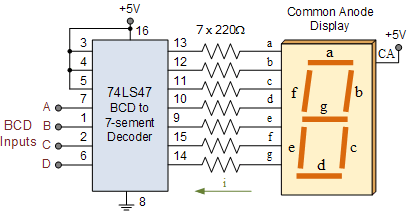
Los polacos probaron con máquinas BINEG que utilizan el negabinario o bases negativas (también existen el negadecimal y el negaternario). Y todo estudiante de informática o telecomunicaciones conoce el BCD (decimal codificado en binario) de 5 bits que se ha usado en todo tipo de sistemas electrónicos, incluyendo visualizadores de siete segmentos y muchas de las antiguas máquinas de IBM. Otros similares con aplicación en comunicaciones son el 2 de 5 y el código Grey. Otro código muy curioso es el biquinario que usaba el Colossus y otras variantes que se vieron en el IBM 650, el UNIVAC y el LARC.
Relacionado:
- Setun, el peculiar ordenador ruso de lógica ternaria
- El Colossus de Bletchley Park
- Cómo contar en binario con las manos (hasta 1.023)
- Un circuito sumador binario de cartulina controlado de forma neumática
- Los ordenadores más raros, raros, raros del mundo
- Una retrocalculadora que funciona a base de relés
- Puertas lógicas construidas con dominós
- Los hackers originales




