Casillas en cruces de filas y columnas
Hay un método bastante básico pero efectivo para localizar algunos números rebeldes que no se descubren empleando los métodos de eliminación. A falta de una denominación estándar podría llamarse «casillas que hay en cruces de filas, columnas», o simplemente «cruces». Consiste en fijarse en una casilla que esté situada en un cruce de filas y columnas en las que haya muchos números y comprobarlos todos por orden, del 1 al 9, observando cuáles no pueden ser porque ya están en esas filas o columnas, para ver si con un poco de suerte sólo queda uno.
(5a) En este diagrama diseñado al efecto se puede ver que hay una casilla en el cruce (intersección) de dos filas y columnas donde hay bastantes números. En realidad todas las filas y columnas tienen cruces, pero sólo hay que fijarse en las abundan los números. Partiendo de esa casilla basta revisar todos los números de esa fila y esa columna y adivinar cuál es el número que falta, que por tanto es el único que puede ir ahí: en este caso el 9.
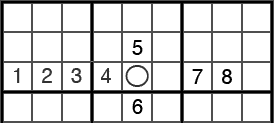
(5b) Este otro ejemplo es más complicado, porque proviene de un Sodoku real, aunque para simplificar sólo se ven los números que interesan para esta técnica. Es difícil de un solo vistazo darse cuenta de que se puede deducir un número a partir de los que hay en el tablero, parecen muy pocos y muy dispersos.
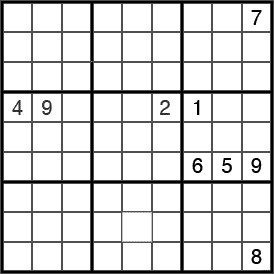
(5b) Sin embargo, basta fijarse en la casilla objetivo, la que está en el cruce de la fila central y la columna de la derecha. Esa es la casilla a comprobar. Numerando por orden rápidamente los ya existentes se ven 1 2 4 9 en la fila y el 7 8 en la columna. Por tanto podría ser cualquiera del grupo 3 5 6. Pero observando la región en que está la casilla «cruce» se observa que el 5 y 6 ya están allí, de modo que sólo queda uno posible, que es la solución: el 3.
Es muy importante al llevar la cuenta de todos los números ya existentes que afectan a los candidatos de una casilla «cruce» fijarse en los de las filas como las columnas como en los de la misma región, como en este ejemplo.
Utilizando esta técnica cuando hay suficientes números es fácil que en muchas casillas sólo quede un número posible, con lo que se pueden avanzar pasos hacia la solución final.

Relacionado:
- Consejos para resolver Sudokus (1), introducción.
- Consejos para resolver Sudokus (2), eliminación por filas y columnas.
- Consejos para resolver Sudokus (3), eliminación por regiones.
- Consejos para resolver Sudokus (4), números que faltan.
- Consejos para resolver Sudokus (5), casillas en cruces de filas y columnas.
- Consejos para resolver Sudokus (6), parejas de números en la misma fila/columna.


