Consejos para resolver Sudokus (6)

Por @Alvy — 23 de Agosto de 2005

Parejas de números

Nota: la versión original de este consejo #6 empleaba un tablero algo confuso, de modo que se ha cambiado completamente por otro con un ejemplo más adecuado.

Este truco se puede utilizar con bastante frecuencia y permite llevar los razonamientos lógicos un poquito más allá para descubrir la posición de nuevos números en el tablero de una forma realmente peculiar. Se basa en encontrar números posibles «emparejados», normalmente en la misma fila o columna.

(6a) En este diagrama faltan bastantes números. A primera vista en la primera región habría que situar los números 4 7 8, pero cada uno pueden tener al menos dos posiciones posibles. Nada que hacer de momento. En la región intermedia izquierda faltan seis números: 1 2 3 4 7 8 y los cruces de números con las otras regiones tampoco parecen ayudar mucho aunque hay algunas eliminaciones. En la región inferior faltan también cinco números. Demasiados. Y no hay métodos de eliminación directa que sirvan en este caso. ¿Se puede deducir la posición de algún número más en esas regiones teniendo en cuenta únicamente los que se ven en el tablero?

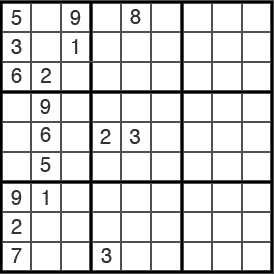
(6b) Para seguir la pista a todos esos números «posibles» en cada casilla se suelen escribir con lápiz, en pequeñito, los dígitos correspondientes. Aunque cada persona lo hace de forma diferente, una forma es la que muestra la imagen. A partir de la eliminación de algunas casillas de las misma fila o columna, con los números 2 y 3 se escribe 23 en la primera casilla y 23 en la segunda. Eso quiere decir que en esas casillas pueden ir el 2 o el 3, pero no está claro en qué orden. (Hay quien escribe 23/32, o bien emplea pequeños puntitos en las posiciones, o utiliza un lápiz de otro color.)

El truco para las parejas de números, explicado como una regla, es el siguiente: Dos números posibles en pareja que estén en dos únicas casillas en la misma fila, columna o región, se comportan de modo que se pueden eliminar esos números de todas las demás casillas de esa fila, columna o región, aunque no se sepa exactamente todavía dónde va cada uno de ellos. La razón para esto es la siguiente: si son dos números y sólo hay dos sitios posibles (aunque no se sepa en qué orden) no puede ir ningún otro número distinto en esas casilas. Si en la primera casilla resultara ir otro número distinto a los de la pareja, entonces el primero de los números de la pareja se podría colocar en la segunda casilla, pero faltaría una casilla más para el segundo número - y como esos dos números sólo eran posibles esas dos casillas, se llegaría a una cotradicción.

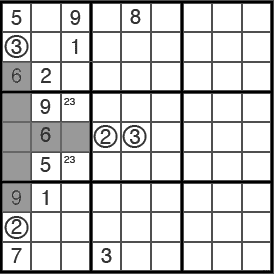
De cara a los razonamientos, esas dos casillas se comportan casi como una (la «casilla de la pareja») y por eso si además las casillas están en la misma fila o columna se pueden eliminar esos mismos números individuales de todas las demás casillas de esa fila/columna (si forman fila, los de la fila, si forman columna, los de la columna). La única condición es que sean una pareja de dos números y estén en sólo dos casillas.

Nota: Esta técnica también funciona con tríos de números, empleándose el mismo razonamiento, incluso si alguno de los tríos está incompleto, como también ha apuntado un lector en los comentarios.

En esa misma región del diagrama 6b se podrían haber escrito más números posibles. Por ejemplo las casillas de la columna de la izquierda podrían llevar todas el 148 porque esos números también faltan en esa región. Y donde se ha escrito 23/23 se podría haber escrito 23478/23478, pero según la regla 4, 7 y 8 son innecesarios porque 23 es la pareja correcta para esas dos casillas (cualquier pareja formada por 4, 7 y 8 no lo sería porque también son posibles en otras muchas casillas, no sólo en esas dos, de modo que no cumplen la regla).

(6c) Utilizando la regla de las parejas se puede considerar que en las dos casillas marcadas van el 2 y el 3 aunque no se sepa en qué orden. Esto permite por ejemplo trazar con ellos una línea vertical hacia abajo para eliminar unas cuantas casillas de la región inferior. Como además hay un 3 a la derecha que facilita la eliminación de otra casilla, resulta que se puede poner un 3 en la casilla central

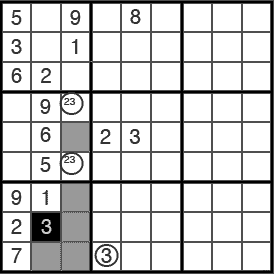
Como puede verse, el efecto de esta técnica es realmente curioso: se ha colocado un 3 en la última región sin que se sepa realmente hasta más adelante dónde va situado el 3 de la región intermedia, que es el que ha ayudado a eliminar las otras opciones.

(6d) Aprovechando de nuevo la formación de la pareja 23/23 de la región central se puede observar que el 7 de abajo elimina varias de las casillas de la región central, y se puede situar allí también un 7 como definitivo.

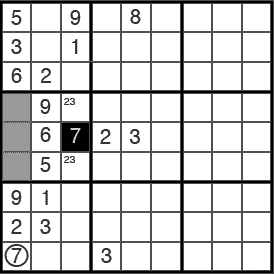
Esto demuestra por qué esta técnica es tan poderosa: ha permitido inculso situar un número en una región donde apenas había ninguno, con solo otro número de ayuda y sin siquiera conocer con exactitud dónde van los componentes de la pareja que sirve de guía.

Importante:A veces la fila, columna o región donde está la pareja sólo tiene otra casilla libre (hay tres en total). En ese caso se deduce directamente cuál es el número que falta, el «tercero en discordia» porque de los tres posibles los dos primeros (aunque no se conozca el orden) tendrás sus casillas emparejadas, de las que no pueden escapar.

Las parejas de números no sirven para hacer barridos de eliminación por filas o columnas cuando las casillas de la pareja no están situadas en la misma fila/columna (en diagonal). En ese caso sólo sirven para eliminar otros números posibles de la misma región, lo cual no obstante también puede ser útil. Cuando están en la posición adecuada, eliminan muchas más casillas posibles y ayudan a encontrar más números.

Relacionado:

Consejos para resolver Sudokus (1), introducción.
Consejos para resolver Sudokus (2), eliminación por filas y columnas.
Consejos para resolver Sudokus (3), eliminación por regiones.
Consejos para resolver Sudokus (4), números que faltan.
Consejos para resolver Sudokus (5), casillas en cruces de filas y columnas.
Consejos para resolver Sudokus (6), parejas de números.