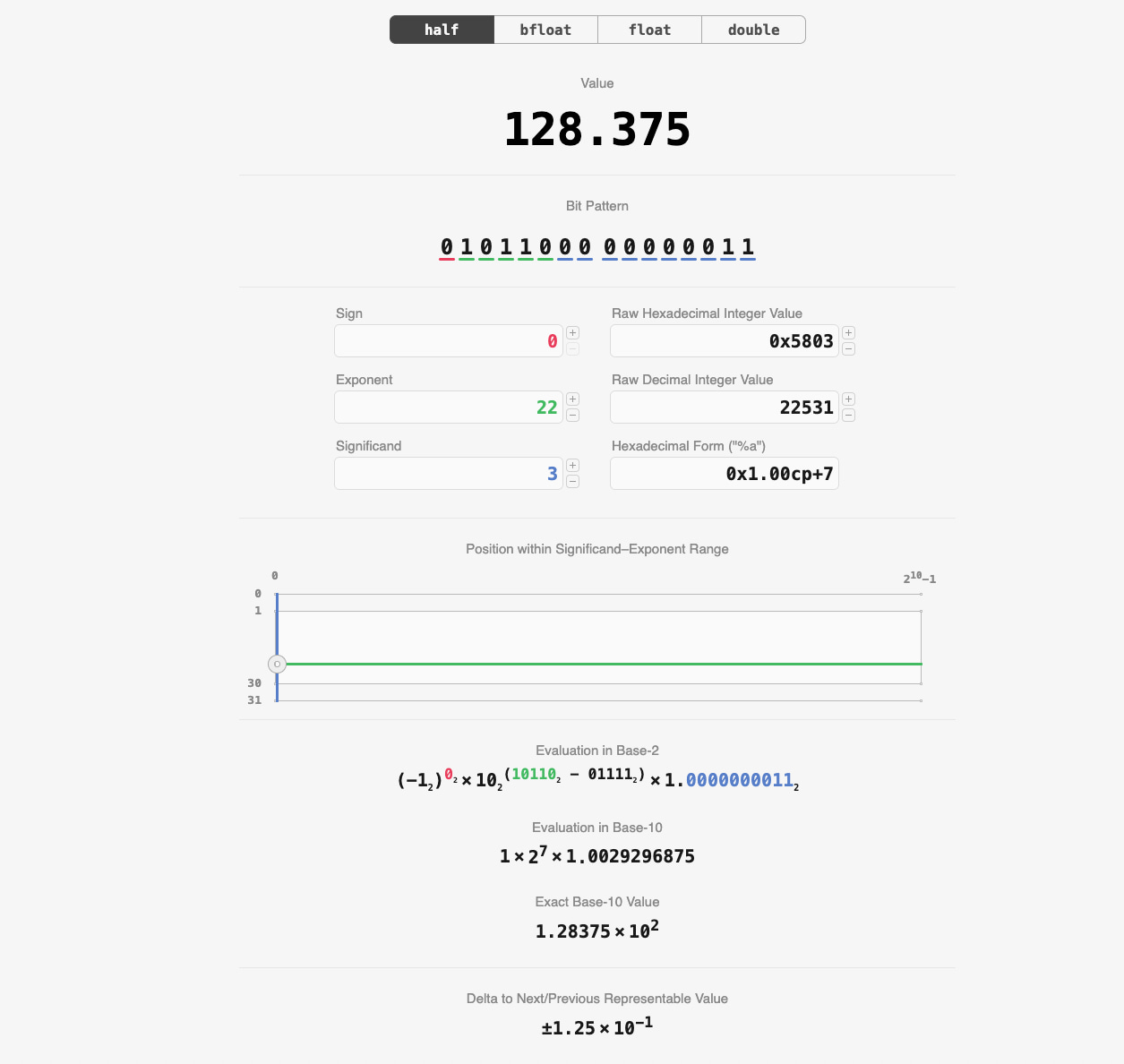
Los números en coma flotante (IEEE 754) están presentes en todo dispositivo moderno que se precie, pero el cómo funcionan tiene su intríngulis. Nuestro admirado Bartosz Ciechanowski los analizó hace años en un artículo y tiene una herramienta llamada float.exposed que es una representación visual interactiva/calculadora de cómo son esos números, su valor decimal, hexadecimal, binario y sus diversos componentes.
Allí se ven con ejemplos claros por qué algunos valores como 0,2 no pueden representarse con exactitud y cómo aparecen fenómenos como los infinitos, los ceros con signo y los NaN (Not-a-number).
En esencia, un número en coma flotante es una notación científica binaria con un par de limitaciones: el número de dígitos en la mantisa (o significando) y el rango del exponente. Por ejemplo, un número de coma flotante (float) de 32 bits tiene 24 bits de mantisa y un rango de exponente que va de [−126, +127]. Eso permite representar enteros hasta 224 (16.777.216), pero deja fuera números intermedios como 16.777.217. (Prueba a ponerlo en la calculadora.)
Además de que los float de simple precisión ocupan 32 bits; un float doble son 64 bits con 53 dígitos de precisión y rango [−1.022, +1.023] y un float de media precisión, 16 bits con 11 dígitos de mantisa y rango [−14, +15]. Puedes jugar con ello y hacer cambios en la calculadora a ver qué pasa.
Existen valores especiales: ± 0,0, ± ∞ y los NaN (Not a Number). En el caso de los float se pueden codificar más de 8 millones de NaN distintos, y en los dobles más de 4,5 cuatrillones.
El máximo valor representable en un float es 3,40282347×1038, mientras que el mínimo normal es 1,17549435×10-38. Gracias a los subnormales (se llaman así) se puede llegar a valores aún más pequeños, aunque con menor precisión.
Estos límites explican anomalías clásicas como que 0,1 o 0,2 no tienen una representación exacta, o que al operar aparezcan redondeos inesperados. El diseño del estándar permite operaciones que son coherentes con los infinitos, los ceros con signo, los NaN y también conversiones entre tipos con reglas claras.
Lejos de ser un misterio, el estándar IEEE 754 es una construcción elegante y duradera que define la aritmética digital moderna. Tan es así que en las más complicadas profesiones de matemáticas, ingeniería y programación hay que saber muy bien qué se cuece entre bambalinas para evitar bugs que pueden ser muy difíciles de encontrar.
Otros trabajos de Bartosz Ciechanowski:
- Así funcionan los relojes mecánicos de pulsera
- Así funcionan las cámaras y lentes
- La arquitectura naval explicada paso a paso
- GPS: el Sistema de Posicionamiento Global
Relacionado:




 La meteorología es hoy algo tan común que «hablar del tiempo» se considera la mejor forma de rellenar «silencios incómodos» y de detectar cuándo una conversación está atascada. El caso es la historia de la predicción del tiempo meteorológico, tiene sus raíces en la astrología antes que en la ciencia. Resulta sumamente curioso que el Acta de Brujería de 1735 prohibiera todas las predicciones basadas en medios sobrenaturales, incluyendo pronósticos del tiempo (
La meteorología es hoy algo tan común que «hablar del tiempo» se considera la mejor forma de rellenar «silencios incómodos» y de detectar cuándo una conversación está atascada. El caso es la historia de la predicción del tiempo meteorológico, tiene sus raíces en la astrología antes que en la ciencia. Resulta sumamente curioso que el Acta de Brujería de 1735 prohibiera todas las predicciones basadas en medios sobrenaturales, incluyendo pronósticos del tiempo (